
| 3 |
|
|
|
| DA |
| C′D |
| 3 | ||
3
|
| ||
| 3 |
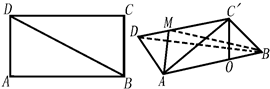
| AD•AC′ |
| DC′ |
3•3
| ||
3
|
| 6 |
| AM |
| AB |
| ||
3
|
| ||
| 3 |


 一课一练一本通系列答案
一课一练一本通系列答案 浙江之星学业水平测试系列答案
浙江之星学业水平测试系列答案科目:高中数学 来源: 题型:
| 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:
(02年北京卷文)(12分)
如图,在多面体ABCD―A1B1C1D1中,上、下底面平行且均为矩形,相对的侧面与同一底面所成的二面角大小相等,上、下底面矩形的长、宽分别为c,d与a,b且a>c,b>d,两底面间的距离为h..
(Ⅰ)求侧面ABB1A1与底面ABCD所成二面角正切值;
(Ⅱ)在估测该多面体的体积时,经常运用近似公式
V估=S中截面?h来计算.已知它的体积公式是
![]() (S上底面+4S中截面+S下底面),
(S上底面+4S中截面+S下底面),
试判断V估与V的大小关系,并加以证明.
(注:与两个底面平行,且到两个底面距离相等的截面称为该多面体的中截面.)

查看答案和解析>>
科目:高中数学 来源:2004年浙江省宁波市十校高三联考数学试卷(解析版) 题型:解答题
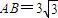 ,BC=3,沿对角线BD将△BCD折起,使点C移到点C',且C'在平面ABD的射影O恰好在AB上,则以C',A,B,D为顶点,构成一个四面体.
,BC=3,沿对角线BD将△BCD折起,使点C移到点C',且C'在平面ABD的射影O恰好在AB上,则以C',A,B,D为顶点,构成一个四面体.查看答案和解析>>
科目:高中数学 来源: 题型:
(09年海淀区二模文)如图,矩形ABCD中,AB=2,BC=4,将△ABD沿对角线BD折起到△A′BD的位置,使点A′在平面BCD内的射影点O恰好落在BC边上,则异面直线A′B与CD所成角的大小为 ;A′D与平面A′BC所成的角的大小为 .

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com