
【题目】如图,在直三棱柱![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() 分别是
分别是![]() ,
,![]() 中点,
中点,![]() 为线段
为线段![]() 上的一个动点.
上的一个动点.
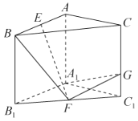
(1)证明:![]() 平面
平面![]() ;
;
(2)当二面角![]() 的余弦值为
的余弦值为![]() 时,证明:
时,证明:![]() .
.
 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】某地区城乡居民储蓄存款年底余额(单位:亿元)如图所示,下列判断一定不正确的是( )
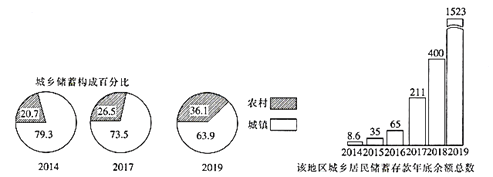
A.城乡居民储蓄存款年底余额逐年增长
B.农村居民的存款年底余额所占比重逐年上升
C.到2019年农村居民存款年底总余额已超过了城镇居民存款年底总余额
D.城镇居民存款年底余额所占的比重逐年下降
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在数学中有这样形状的曲线:![]() .关于这种曲线,有以下结论:
.关于这种曲线,有以下结论:
①曲线![]() 恰好经过9个整点(即横、纵坐标均为整数的点);
恰好经过9个整点(即横、纵坐标均为整数的点);
②曲线![]() 上任意两点之间的距离都不超过2;
上任意两点之间的距离都不超过2;
③曲线![]() 所围成的“花瓣”形状区域的面积大于5.
所围成的“花瓣”形状区域的面积大于5.
其中正确的结论有:( )
A.①③B.②③C.①②D.①②③
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】数列![]() 的数列
的数列![]() 的首项
的首项![]() ,前n项和为
,前n项和为![]() ,若数列
,若数列![]() 满足:对任意正整数n,k,当
满足:对任意正整数n,k,当![]() 时,
时,![]() 总成立,则称数列
总成立,则称数列![]() 是“
是“![]() 数列”
数列”
(1)若![]() 是公比为2的等比数列,试判断
是公比为2的等比数列,试判断![]() 是否为“
是否为“![]() ”数列?
”数列?
(2)若![]() 是公差为d的等差数列,且是“
是公差为d的等差数列,且是“![]() 数列”,求实数d的值;
数列”,求实数d的值;
(3)若数列![]() 既是“
既是“![]() ”,又是“
”,又是“![]() ”,求证:数列
”,求证:数列![]() 为等差数列.
为等差数列.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的焦点在
的焦点在![]() 轴上,左右顶点分别是
轴上,左右顶点分别是![]() ,以
,以![]() 上的弦
上的弦![]() (
(![]() 异于
异于![]() )为直径作圆
)为直径作圆![]() 恰好过
恰好过![]() ,设直线
,设直线![]() 的斜率为
的斜率为![]() .
.
(1)若![]() ,且
,且![]() 的面积为
的面积为![]() ,求
,求![]() 的方程.
的方程.
(2)若![]() ,求
,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,三棱维![]() 中,平面
中,平面![]() 平面
平面![]() ,
,![]() ,
,![]() ,
,![]() 是棱
是棱![]() 的中点,点
的中点,点![]() 在棱
在棱![]() 上点
上点![]() 是
是![]() 的重心.
的重心.
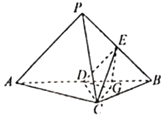
(1)若![]() 是
是![]() 的中点,证明
的中点,证明![]() 面
面![]() ;
;
(2)是否存在点![]() ,使二面角
,使二面角![]() 的大小为
的大小为![]() ,若存在,求
,若存在,求![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2020年冬奥会申办成功,让中国冰雪项目迎来了新的发展机会,“十四冬”作为北京冬奥会前重要的练兵场,对冰雪运动产生了不可忽视的带动作用.某校对冰雪体育社团中甲、乙两人的滑轮、雪合战、雪地足球、冰尜(ga)、爬犁速降及俯卧式爬犁6个冬季体育运动项目进行了指标测试(指标值满分为5分,分高者为优),根据测试情况绘制了如图所示的指标雷达图.则下面叙述正确的是( )
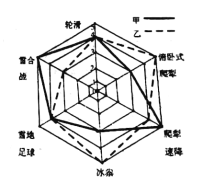
A.甲的轮滑指标高于他的雪地足球指标
B.乙的雪地足球指标低于甲的冰尜指标
C.甲的爬犁速降指标高于乙的爬犁速降指标
D.乙的俯卧式爬犁指标低于甲的雪合战指标
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了检测生产线上某种零件的质量,从产品中随机抽取100个零件,测量其尺寸,得到如图所示的频率分布直方图.若零件尺寸落在区间![]() 之内,则认为该零件合格,否则认为不合格.其中
之内,则认为该零件合格,否则认为不合格.其中![]() ,
,![]() 分别表示样本的平均值和标准差,计算得
分别表示样本的平均值和标准差,计算得![]() (同一组中的数据用该组区间的中点值作代表).
(同一组中的数据用该组区间的中点值作代表).
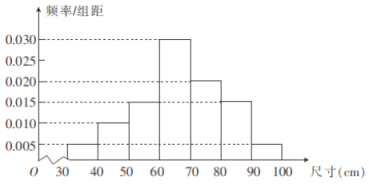
(1)已知一个零件的尺寸是![]() ,试判断该零件是否合格;
,试判断该零件是否合格;
(2)利用分层抽样的方法从尺寸在![]() 的样本中抽取6个零件,再从这6个零件中随机抽取2个,求这2个零件中恰有1个尺寸小于
的样本中抽取6个零件,再从这6个零件中随机抽取2个,求这2个零件中恰有1个尺寸小于![]() 的概率.
的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com