
【题目】已知函数![]() .
.
(1)设在平面直角坐标系中作出![]() 的图象,并写出不等式
的图象,并写出不等式![]() 的解集
的解集![]() .
.
(2)设函数![]() ,
,![]() ,若
,若![]() ,求
,求![]() 的取值范围.
的取值范围.
【答案】(1)函数图象如下图:
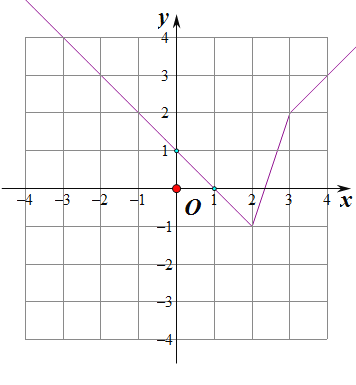
不等式![]() 的解集
的解集![]() ;
;
(2)![]() .
.
【解析】
(1)利用零点法化简函数的解析式,在直角坐标系内,画出函数图象,分类讨论解不等式;
(2)根据(1)对![]() 时,进行分类讨论:
时,进行分类讨论:
当![]() 时,
时,![]() ,根据
,根据![]() 取值的不同范围,利用一次函数的单调性,求出
取值的不同范围,利用一次函数的单调性,求出![]() 的取值范围;
的取值范围;
当![]() 时,
时,![]() ,根据
,根据![]() 取值的不同范围,利用一次函数的单调性,求出
取值的不同范围,利用一次函数的单调性,求出![]() 的取值范围,最后确定
的取值范围,最后确定![]() 的取值范围.
的取值范围.
(1)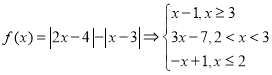 ,画出图象,如下图所示:
,画出图象,如下图所示:

当![]() 时,
时,![]() ;
;
当![]() 时,
时,![]()
当![]() 时,
时,![]() ,所以
,所以
不等式![]() 的解集
的解集![]() .
.
(2)当![]() 时,
时,![]()
当![]() 时,
时,![]() ,显然成立;
,显然成立;
当![]() 时,要想
时,要想![]() ,只需
,只需![]() 即可,也就是
即可,也就是
![]() ;
;
当![]() 时,要想
时,要想![]() ,只需
,只需![]() ,
,
所以当![]() 时,当
时,当![]() ,
,![]() 的取值范围
的取值范围![]() ;
;
当![]() 时,
时,![]() ,
,
当![]() 时,显然
时,显然![]() 不成立;
不成立;
当![]() 时,要想
时,要想![]() ,只需
,只需![]() 不存在这样的
不存在这样的![]() ;
;
当![]() 时,要想
时,要想![]() ,只需
,只需![]() ,
,
所以当![]() 时,当
时,当![]() ,
,![]() 的取值范围是
的取值范围是![]() ,
,
综上所述![]() 的取值范围
的取值范围![]() .
.


科目:高中数学 来源: 题型:
【题目】设函数![]() .
.
(1)若![]() ,判断函数
,判断函数![]() 是否存在极值,若存在,求出极值:若不存在,说明理由:
是否存在极值,若存在,求出极值:若不存在,说明理由:
(2)若![]() 在
在![]() 上恒成立,求实数
上恒成立,求实数![]() 的取值范围:
的取值范围:
(3)若函数![]() 存在两个极值点
存在两个极值点![]() ,证明:
,证明:![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,矩形![]() 中,
中,![]() 为
为![]() 的中点,将
的中点,将![]() 沿直线
沿直线![]() 翻折成
翻折成![]() ,连结
,连结![]() ,
,![]() 为
为![]() 的中点,则在翻折过程中,下列说法中所有正确的是( )
的中点,则在翻折过程中,下列说法中所有正确的是( )
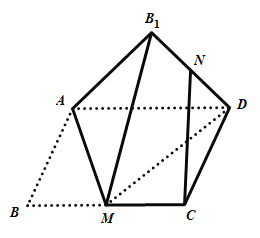
A.存在某个位置,使得![]()
B.翻折过程中,![]() 的长是定值
的长是定值
C.若![]() ,则
,则![]()
D.若![]() ,当三棱锥
,当三棱锥![]() 的体积最大时,三棱锥
的体积最大时,三棱锥![]() 的外接球的表面积是
的外接球的表面积是![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】给出下列四个结论,其中正确的是( )
①从匀速传送的生产流水线上,每30分钟抽取一件产品进行检测,这样的抽样是分层抽样;②“![]() ”成立的必要而不充分条件是“
”成立的必要而不充分条件是“![]() ”;③若样本数据
”;③若样本数据![]() ,
,![]() ,…,
,…,![]() 的标准差为3,则
的标准差为3,则![]() ,
,![]() ,…,
,…,![]() 的方差为145;④
的方差为145;④![]() ,
,![]() ,
,![]() 是向量,则由“
是向量,则由“![]() ”类比得到“
”类比得到“![]() ”的结论是正确的.
”的结论是正确的.
A.①④B.②③C.①③D.②④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在正三棱柱(底面为正三角形的直棱柱)ABC﹣A1B1C1中,已知AB=AA1=2,点Q为BC的中点.
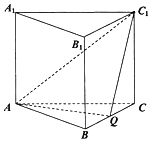
(1)求证:平面AQC1⊥平面B1BCC1;
(2)求直线CC1与平面AQC1所成角的正切值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一家小微企业生产某种小型产品的月固定成本为1万元,每生产1万件需要再投入2万元,假设该企业每个月可生产该小型产品![]() 万件并全部销售完,每万件的销售收入为
万件并全部销售完,每万件的销售收入为![]() 万元,且每生产1万件政府给予补助
万元,且每生产1万件政府给予补助![]() 万元.
万元.
(1)求该企业的月利润![]() (万元)关于月产量
(万元)关于月产量![]() (万件)的函数解析式;
(万件)的函数解析式;
(2)若月产量![]() 万件时,求企业在生产这种小型产品中所获得的月利润最大值(万元)及此时的月生产量值(万件).
万件时,求企业在生产这种小型产品中所获得的月利润最大值(万元)及此时的月生产量值(万件).
(注:月利润=月销售收入+月政府补助![]() 月总成本)
月总成本)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的离心率为
的离心率为![]() ,与
,与![]() 轴交于点
轴交于点![]() ,
,![]() ,过
,过![]() 轴上一点
轴上一点![]() 引
引![]() 轴的垂线,交椭圆
轴的垂线,交椭圆![]() 于点
于点![]() ,
,![]() ,当
,当![]() 与椭圆右焦点重合时,
与椭圆右焦点重合时,![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)设直线![]() 与直线
与直线![]() 交于点
交于点![]() ,是否存在定点
,是否存在定点![]() 和
和![]() ,使
,使![]() 为定值.若存在,求
为定值.若存在,求![]() 、
、![]() 点的坐标;若不存在,说明理由.
点的坐标;若不存在,说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com