
【题目】已知函数![]() ,曲线
,曲线![]() 在点
在点![]() 处的切线平行于
处的切线平行于![]() 轴.
轴.
(1)求![]() 的单调区间;
的单调区间;
(2)证明:当![]() 时,
时, ![]() .
.
【答案】(1)递减区间为![]() ,递增区间为
,递增区间为![]() .(2)见解析
.(2)见解析
【解析】试题分析:(1)求得![]() 的导数,由题意可得
的导数,由题意可得![]() ,解方程可得
,解方程可得![]() ,由导数与单调性的关系,结合
,由导数与单调性的关系,结合![]() ,可得
,可得![]() 的单调区间;(2)讨论①当
的单调区间;(2)讨论①当![]() 时,求得
时,求得![]() 的最小值,可得结论成立;②当
的最小值,可得结论成立;②当![]() 时,设
时,设![]() ,求出导数,构造函数
,求出导数,构造函数![]() ,求得导数,判断单调性,可得
,求得导数,判断单调性,可得![]() 最小值,即可得证.
最小值,即可得证.
试题解析:(1)因为![]() ,
, ![]() ,
,
依题意得![]() ,即
,即![]() ,解得
,解得![]() .
.
所以![]() ,显然
,显然![]() 在
在![]() 单调递增且
单调递增且![]() ,
,
故当![]() 时,
时, ![]() ;当
;当![]() 时,
时, ![]() .
.
所以![]() 的递减区间为
的递减区间为![]() ,递增区间为
,递增区间为![]() .
.
(2)①当![]() 时,由(1)知,当
时,由(1)知,当![]() 时,
时, ![]() 取得最小值
取得最小值![]() .
.
又![]() 的最大值为
的最大值为![]() ,故
,故![]() .
.
②当![]() 时,设
时,设![]() ,
,
所以![]() ,
,
令![]() ,
, ![]() ,则
,则![]() ,
,
当![]() 时,
时, ![]() ,
,![]() ,所以
,所以![]() ,
,
当![]() 时,
时, ![]() ,
, ![]() ,所以
,所以![]() ,
,
所以当![]() 时,
时, ![]() ,故
,故![]() 在
在![]() 上单调递增,
上单调递增,
又![]() ,所以当
,所以当![]() 时,
时, ![]() ; 当
; 当![]() 时,
时, ![]() .
.
所以![]() 在
在![]() 上单调递减,在
上单调递减,在![]() 上单调递增,
上单调递增,
所以当![]() 时,
时, ![]() 取得最小值
取得最小值![]() ,
,
所以![]() ,即
,即![]() .
.
综上,当![]()
![]() 时,
时, ![]() .
.


 状元及第系列答案
状元及第系列答案 同步奥数系列答案
同步奥数系列答案科目:高中数学 来源: 题型:
【题目】已知函数f(x)=log ![]() (x2﹣ax+b). (Ⅰ)若函数f(x)的定义域为(﹣∞,2)∪(3,+∞),求实数a,b的值;
(x2﹣ax+b). (Ⅰ)若函数f(x)的定义域为(﹣∞,2)∪(3,+∞),求实数a,b的值;
(Ⅱ)若f(﹣2)=﹣3且f(x)在(﹣∞,﹣1]上为增函数,求实数b的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列四组函数,两个函数相同的是( )
A.f(x)= ![]() ,g(x)=x
,g(x)=x
B.f(x)=log33x , g(x)= ![]()
C.f(x)=( ![]() )2 , g(x)=|x|
)2 , g(x)=|x|
D.f(x)=x,g(x)=x0
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某畜牧站为了考查某种新型药物预防动物疾病的效果,利用小白鼠进行试验,得到如下丢失数据的![]() 列联表
列联表
患病 | 未患病 | 总计 | |
没服用药 | 20 | 30 | 50 |
服用药 |
|
| 50 |
总计 |
|
| 100 |
设从没服用药的小白鼠中任取两只,未患病的动物数为![]() ,从服用药物的小白鼠中任取两只,未患病的动物数为
,从服用药物的小白鼠中任取两只,未患病的动物数为![]() ,得到如下比例关系:
,得到如下比例关系:![]()
(1)求出![]() 列联表中数据
列联表中数据![]() ,
,![]() ,
,![]() ,
,![]() 的值
的值
(2)是否有![]() 的把握认为药物有效?并说明理由
的把握认为药物有效?并说明理由
(参考公式:![]() ,当
,当![]() 时,有
时,有![]() 的把握认为A与B有关;
的把握认为A与B有关;![]() 时,有
时,有![]() 的把握认为A与B有关.
的把握认为A与B有关.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校选择高一年级三个班进行为期二年的教学改革试验,为此需要为这三个班各购买某种设备1台.经市场调研,该种设备有甲乙两型产品,甲型价格是3000元/台,乙型价格是2000元/台,这两型产品使用寿命都至少是一年,甲型产品使用寿命低于2年的概率是![]() ,乙型产品使用寿命低于2年的概率是
,乙型产品使用寿命低于2年的概率是![]() .若某班设备在试验期内使用寿命到期,则需要再购买乙型产品更换.
.若某班设备在试验期内使用寿命到期,则需要再购买乙型产品更换.
(1)若该校购买甲型2台,乙型1台,求试验期内购买该种设备总费用恰好是10000元的概率;
(2)该校有购买该种设备的两种方案, ![]() 方案:购买甲型3台;
方案:购买甲型3台; ![]() 方案:购买甲型2台乙型1台.若根据2年试验期内购买该设备总费用的期望值决定选择哪种方案,你认为该校应该选择哪种方案?
方案:购买甲型2台乙型1台.若根据2年试验期内购买该设备总费用的期望值决定选择哪种方案,你认为该校应该选择哪种方案?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列各组函数中,表示同一函数的是( )
A.f(x)= ![]() ,g(x)=(
,g(x)=( ![]() )2
)2
B.f(x)=(x﹣1)0 , g(x)=1
C.f(x) ![]() ,g(x)=x+1
,g(x)=x+1
D.f(x)= ![]() ,g(t)=|t|
,g(t)=|t|
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】人耳的听力情况可以用电子测听器检测,正常人听力的等级为0-25![]() (分贝),并规定测试值在区间
(分贝),并规定测试值在区间![]() 为非常优秀,测试值在区间
为非常优秀,测试值在区间![]() 为优秀.某班50名同学都进行了听力测试,所得测试值制成频率分布直方图:
为优秀.某班50名同学都进行了听力测试,所得测试值制成频率分布直方图:

(Ⅰ)现从听力等级为![]() 的同学中任意抽取出4人,记听力非常优秀的同学人数为
的同学中任意抽取出4人,记听力非常优秀的同学人数为![]() ,求
,求![]() 的分布列与数学期望;
的分布列与数学期望;
(Ⅱ)在(Ⅰ)中抽出的4人中任选一人参加一个更高级别的听力测试,测试规则如下:四个音叉的发生情况不同,由强到弱的次序分别为1,2,3,4.测试前将音叉随机排列,被测试的同学依次听完后给四个音叉按发音的强弱标出一组序号![]() ,
, ![]() ,
, ![]() ,
, ![]() (其中
(其中![]() ,
, ![]() ,
, ![]() ,
, ![]() 为1,2,3,4的一个排列).若
为1,2,3,4的一个排列).若![]() 为两次排序偏离程度的一种描述,
为两次排序偏离程度的一种描述, ![]() ,求
,求![]() 的概率.
的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】本着健康、低碳的生活理念,租自行车骑游的人越来越多.某自行车租车点的收费标准是每年每次租时间不超过两小时免费,超过两个小时的部分每小时收费2元(不足1小时的部分按1小时计算).现有甲、乙两人独立来该租车点租车骑游(各租一车一次).设甲、乙不超过两小时还车的概率分别为![]() ,
, ![]() ;两小时以上且不超过三小时还车的概率为
;两小时以上且不超过三小时还车的概率为![]() ,
, ![]() ;两人租车时间都不会超过四小时.
;两人租车时间都不会超过四小时.
(1)求甲、乙都在三到四小时内还车的概率和甲、乙两人所付租车费相同的概率;
(2)设甲、乙两人所付的租车费用之和为随机变量![]() ,求
,求![]() 的分布列与数学期望
的分布列与数学期望![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】共享单车是指由企业在校园、公交站点、商业区、公共服务区等场所提供的自行车单车共享服务,由于其依托“互联网+”,符合“低碳出行”的理念,已越来越多地引起了人们的关注.某部门为了对该城市共享单车加强监管,随机选取了100人就该城市共享单车的推行情况进行问卷调查,并将问卷中的这100人根据其满意度评分值(百分制)按照[50,60),[60,70),…,[90,100] 分成5组,制成如图所示频率分直方图.
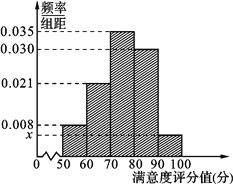
(Ⅰ) 求图中![]() 的值;
的值;
(Ⅱ) 已知满意度评分值在[90,100]内的男生数与女生数的比为2:1,若在满意度评分值为[90,100]的人中随机抽取2人进行座谈,求所抽取的两人中至少有一名女生的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com