练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    △ABC中，AB边的高为CD，若
    CB
    =
    a
    ，
    CA
    =
    b
    ，
    a
    •
    b
    =0，|
    a
    |=1，|
    b
    |=2，则
    AD
    =
    4
    5
    a
    -
    4
    5
    b
    4
    5
    a
    -
    4
    5
    b
    ．
    分析：由已知，先容易得出∠C为直角，利用勾股定理得出AB，AD长，利用向量共线定理得出
    AD
    =
    4
    5
    AB
    =
    4
    5
    (
    a
    -
    b
    )    =
    4
    5
    a
    -
    4
    5
    b
    解答：解：由已知，∠C为直角，如图所示：
    由勾股定理得出AB=
    		5
    ，CD=
    1×2
    		5
    =
    2
    		5

    所以在RT△BDC中，利用勾股定理求出AD=
    4
    		5

    所以
    AD
    =
    4
    5
    AB
    =
    4
    5
    (
    a
    -
    b
    )    =
    4
    5
    a
    -
    4
    5
    b

    故答案为：
    4
    5
    a
    -
    4
    5
    b
    点评：本题考查平面向量基本定理及其意义，考查了向量共线定理，向量减法的几何意义．考查数形结合的思想，转化的能力．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    △ABC中，AB边的高为CD，若
    CB
    =
    a
    ，
    CA
    =
    b
    ，
    a
    •
    b
    =0，|
    a
    |=1，|
    b
    |=2，则
    AD
    =（　　）

    查看答案和解析>>

    科目：高中数学 来源：2012-2013学年山东省临沂市映达高考补习学校高三一轮复习期中迎考数学模拟试卷1（理科）（解析版） 题型：选择题

    △ABC中，AB边的高为CD，若=，=，•=0，||=1，||=2，则=（ ）
    A．
    B．
    C．
    D．

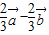
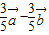
    查看答案和解析>>

    科目：高中数学 来源：2012-2013学年黑龙江省大庆实验中学高二（上）期初数学试卷（理科）（解析版） 题型：选择题

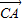    △ABC中，AB边的高为CD，若=，=，•=0，||=1，||=2，则=（ ）
    A．
    B．
    C．
    D．

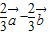
    查看答案和解析>>

    科目：高中数学 来源：2012年全国统一高考数学试卷（文科）（大纲版）（解析版） 题型：选择题

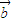    △ABC中，AB边的高为CD，若=，=，•=0，||=1，||=2，则=（ ）
    A．
    B．
    C．
    D．

    查看答案和解析>>

    同步练习册答案