
����Ŀ�����¹ڲ�����Űȫ��Ĵ�������ǰ���й�ȫ���ߣ���־�ɳǣ�ȡ���˽���ʤ����Ϊ���������˰�������.Ϊ��ףս�߳ɹ����Ҿ���ָ����ã�ij����ƽ̨���̼ҽ����н���������˿�������ÿ��600Ԫ����ѡ��ֱ�ӷ���60Ԫ�ֽ��μ�һ�δ��ⷵ�֣����ⷵ�ֹ������£����Դ���������ѡ��һ��Ŀ�ù˿���ʱ���𣬼���˿ʹ�Եĸ��ʶ���0.4���������Ŀ�Ϳɻ��120Ԫ���ֽ��������������û�з���.����˿ʹ���Ľ�������.
��1����ij�˿�������1800Ԫ����Ϊ����ƽ̨���̼ң�ͨ�����ֵ����������жϣ���ϣ���˿�ֱ��ѡ��180Ԫ�ֽ𣬻���ѡ��μ�3�δ��ⷵ�֣�
��2����ij�˿�������7200Ԫ���Ҷ�ѡ��μӴ��ⷵ�֣������ù˿ʹ�Զ��ٴθ���������п��ܷ��ض����ֽ�
���𰸡���1���̼�ϣ���˿ͲμӴ��ⷵ�֣���2���ù˿ʹ��5�εĸ���������п��ܷ���![]() Ԫ�ֽ�.
Ԫ�ֽ�.
��������
��1����![]() ��ʾ�˿������δ����д�ԵĴ��������ö���ֲ�����ɵ�
��ʾ�˿������δ����д�ԵĴ��������ö���ֲ�����ɵ�![]() ���Ӷ��ɵù˿������δ����пɻ�õķ��ֽ�������Ϊ
���Ӷ��ɵù˿������δ����пɻ�õķ��ֽ�������Ϊ![]() Ԫ���Ӷ��ɵ��̼ҵ���ȷѡ��.
Ԫ���Ӷ��ɵ��̼ҵ���ȷѡ��.
��2������֪�˿Ϳ��Բμ�12�δ��ⷵ�֣������д�ԵĴ���Ϊ![]() .���ö���ֲ��ɵ�
.���ö���ֲ��ɵ�![]() ��
��![]() ��1��2������12����
��1��2������12���� �ɵ�
�ɵ�![]() ���Ӷ��ɵøù˿ʹ��5�εĸ�����ʿɵ����п��ܷ��ص��ֽ��.
���Ӷ��ɵøù˿ʹ��5�εĸ�����ʿɵ����п��ܷ��ص��ֽ��.
��1����![]() ��ʾ�˿������δ����д�ԵĴ�����
��ʾ�˿������δ����д�ԵĴ�����
���ڹ˿�ÿ�δ���Ľ����������ģ���![]() ��.
��.
����![]() .
.
���ڹ˿�ÿ���һ��ɻ��120Ԫ���ֽ�������˸ù˿������δ����пɻ�õķ��ֽ�������Ϊ![]() Ԫ.���ڹ˿Ͳμ����δ��ⷵ�ֵ�����144ԪС��ֱ�ӷ��ֵ�180Ԫ�������̼�ϣ���˿ͲμӴ��ⷵ��..
Ԫ.���ڹ˿Ͳμ����δ��ⷵ�ֵ�����144ԪС��ֱ�ӷ��ֵ�180Ԫ�������̼�ϣ���˿ͲμӴ��ⷵ��..
��2������֪�˿Ϳ��Բμ�12�δ��ⷵ�֣������д�ԵĴ���Ϊ![]() .
.
���ڹ˿ʹ���Ľ����������ģ���![]() ��.
��.
![]() ��
��![]() ��1��2������12
��1��2������12
����˿ʹ��![]() �εĸ������
�εĸ������
����
����![]() ������
������![]() ������
������![]() ���.
���.
���Ըù˿ʹ��5�εĸ���������п��ܷ���![]() Ԫ�ֽ�.
Ԫ�ֽ�.


 �����������Ů��ͯ������ϵ�д�
�����������Ů��ͯ������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ѷ���![]() ��ʾ��������Ϊ����
��ʾ��������Ϊ����![]() ��ͼ�������н�����ȷ���ǣ� ��
��ͼ�������н�����ȷ���ǣ� ��
��![]() ��R�ϵ����ݼ�
��R�ϵ����ݼ�
��![]() ��ͼ�����ԭ��Գ�
��ͼ�����ԭ��Գ�
��![]() ��ͼ���ϵĵ㵽����ԭ��ľ������СֵΪ3
��ͼ���ϵĵ㵽����ԭ��ľ������СֵΪ3
�ܺ���![]() ���������
���������
A.�٢�B.�٢ڢ�C.�٢ۢ�D.�٢ڢۢ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����f��x����axex��g��x����x2+2x+b��������y��f��x��������y��g��x��������P��1��c�������ڵ�P������ͬ������l��
����������l�ķ��̣�
����������x�IJ���ʽk[ef��x��]��g��x��������x��[��1��+�������������ʵ��k��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ס��ҡ������˲μӾ�����Ϸ��һ��������Ŀ��ÿ�˻ش�һ��Ϊ���ֹ�ƽ���ƶ����¹���
�ٵ�һ�ֻش�˳��Ϊ�ס��ҡ������ڶ��ֻش�˳��Ϊ�ҡ������ף������ֻش�˳��Ϊ�����ס��ң������ֻش�˳��Ϊ�ס��ҡ������������水�˹����������½��У�
�ڵ�һ�˻ش���ȷʱ��������������һ���ش���ȷ����ʤ��.
��֪��ÿ�μش���ȷ�ĸ���Ϊ![]() ���һش���ȷ�ĸ���Ϊ
���һش���ȷ�ĸ���Ϊ![]() �����ش���ȷ�ĸ���Ϊ
�����ش���ȷ�ĸ���Ϊ![]() �������˻ش�ÿ�����������.
�������˻ش�ÿ�����������.
��1����һ��������ȫ�ش���ȷ�ĸ��ʣ�
��2���ֱ�����ڵ�һ�֡��ڶ��֡�������ʤ���ĸ��ʣ�
��3����![]() Ϊ���ڵ�
Ϊ���ڵ�![]() ��ʤ���ĸ��ʣ�
��ʤ���ĸ��ʣ�![]() Ϊ���ڵ�
Ϊ���ڵ�![]() ��ʤ���ĸ��ʣ���
��ʤ���ĸ��ʣ���![]() ��
��![]() �����Ƚ�
�����Ƚ�![]() ��
��![]() �Ĵ�С.
�Ĵ�С.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������![]() �У������
�У������![]() �DZ߳�Ϊ2���������Σ�
�DZ߳�Ϊ2���������Σ�![]() ��
��![]() ����
����![]() ����
����![]() �ֱ�Ϊ
�ֱ�Ϊ![]() ��
��![]() ���е�.
���е�.
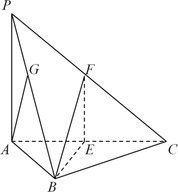
��1����֤��ƽ��![]() ƽ��
ƽ��![]() ��
��
��2�����߶�![]() ���Ƿ���ڵ�
���Ƿ���ڵ�![]() ��ʹ������
��ʹ������![]() ���Ϊ
���Ϊ![]() �������ڣ�ȷ����
�������ڣ�ȷ����![]() ��λ�ã��������ڣ���˵������.
��λ�ã��������ڣ���˵������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����![]() ������
������![]() ��
��
��1����![]() �ĵ������䣻
�ĵ������䣻
��2�����������![]() ���ܴ���
���ܴ���![]() ��ʹ��
��ʹ��![]() ����ʵ��
����ʵ��![]() ��ֵ��
��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪ij��![]() ��ȫ���̶��ʲ�Ͷ���Լ���������ͼ��ʾ��������˵���������ǣ� ��
��ȫ���̶��ʲ�Ͷ���Լ���������ͼ��ʾ��������˵���������ǣ� ��
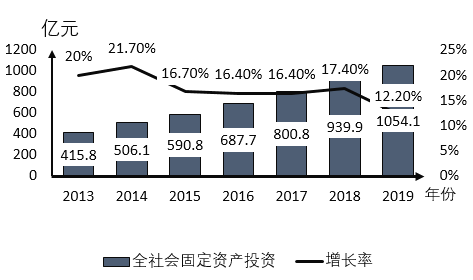
A.��2013�굽2019��ȫ���̶��ʲ���Ͷ�ʴ��ڲ���������״̬
B.��2013�굽2019��ȫ���̶��ʲ�Ͷ�ʵ�ƽ��ֵΪ![]() ��Ԫ
��Ԫ
C.����ȫ���̶��ʲ�Ͷ����������ߵ����Ϊ2014��
D.2016�굽2017��ȫ���̶��ʲ���������Ϊ0
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����Ϊ2��![]() �У�
��![]() ��
��![]() �ֱ���
�ֱ���![]() ��
��![]() ���е㣬��
���е㣬��![]() ��ֱ��EF�ϣ���
��ֱ��EF�ϣ���![]() ����Сֵ�ǣ� ��
����Сֵ�ǣ� ��
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ƽ��ֱ������ϵ![]() �У�����
�У�����![]() �IJ�������Ϊ
�IJ�������Ϊ ��
��![]() ������������
Ϊ������������![]() �IJ�������Ϊ
�IJ�������Ϊ![]() ��
��![]() Ϊ��������������ԭ��Ϊ���㣬
Ϊ��������������ԭ��Ϊ���㣬![]() ��������Ϊ���Ὠ��������ϵ.
��������Ϊ���Ὠ��������ϵ.
��1��������![]() ����ͨ���̺�����
����ͨ���̺�����![]() �ļ����귽�̣�
�ļ����귽�̣�
��2������![]() ������
������![]() ����
����![]() ��
��![]() ���㣬����
���㣬����![]() ������
������![]() ���ڵ�
���ڵ�![]() ����
����![]() �����Ϊ1����
�����Ϊ1����![]() ��ֵ.
��ֵ.
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com