
解法一:如图,设所求直线的方程为y-1=k(x-2),
代入椭圆方程并整理,得
(4k2+1)x2-8(2k2-k)x+4(2k-1)2-16=0,
又设直线与椭圆的交点为A(x1,y1),B(x2,y2),
则x1、x2是上面的方程的两个根,
∴x1+x2=![]()
∵P为弦AB的中点,
∴![]()
解得k=-![]() ,
,
∴所求直线的方程为x+2y-4=0.
解法二:
设直线与椭圆交点为A(x1,y1),B(x2,y2),则
∵P为弦AB的中点,
∴x1+x2=4,y1+y2=2.
又∵A、B在椭圆上,
∴x12+4y12=16,x22+4y22=16.
两式相减,得(x12-x22)+4(y12-y22)=0,
即(x1+x2)(x1-x2)+4(y1+y2)(y1-y2)=0.
∴![]()
即kAB=-![]() .
.
∴所求直线方程为y-1=-![]() (x-2),
(x-2),
即x+2y-4=0.
解法三:
设所求直线与椭圆的一交点为A(x,y),另一交点为B(4-x,2-y),则
∵A、B在椭圆上,
∴x2+4y2=16, ①
(4-x)2+4(2-y)2=16. ②
从而A、B在方程①-②的图形x+2y-4=0上,而过A、B的直线只有一条,
∴所求直线的方程为x+2y-4=0.绿色通道:中点弦问题求解关键在于充分利用“中点”这一条件,灵活运用中点坐标公式及根与系数的关系.例题中的方法一是设出方程,根据中点坐标求出k;方法二是“设而不求”,即设出交点坐标,代入方程,整体求出斜率;方法三最简便,但是不容易想出.


 第三学期赢在暑假系列答案
第三学期赢在暑假系列答案 学练快车道快乐假期暑假作业新疆人民出版社系列答案
学练快车道快乐假期暑假作业新疆人民出版社系列答案科目:高中数学 来源: 题型:
| 3 | 2 |
查看答案和解析>>
科目:高中数学 来源:广西南宁二中2012届高三12月月考数学理科试题 题型:044
已知椭圆![]() ,过点
,过点![]() P作椭圆C的两条切线PM,PN,切点分别为M,N,△PMN为等边三角形.
P作椭圆C的两条切线PM,PN,切点分别为M,N,△PMN为等边三角形.
(1)求椭圆C的离心率;
(2)过椭圆C的左焦点F作斜率为1的直线l与椭圆C交于A、B两点,D为椭圆C上任意一点,求证:存在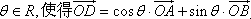 成立.
成立.
查看答案和解析>>
科目:高中数学 来源:2009-2010学年北京市昌平区高二(上)期末数学试卷(理科)(解析版) 题型:解答题
 ),两个焦点分别为F1(-1,0),F2(1,0).
),两个焦点分别为F1(-1,0),F2(1,0).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com