
【题目】公元263年左右,我国数学有刘徽发现当圆内接多边形的边数无限增加时,多边形的面积可无限逼近圆的面积,并创立了割圆术,利用割圆术刘徽得到了圆周率精确到小数点后面两位的近似值3.14,这就是著名的“徽率”.某同学利用刘徽的“割圆术”思想设计了一个计算圆周率的近似值的程序框图如图,则输出S的值为 (参考数据:sin15°=0.2588,sin7.5°=0.1305)( )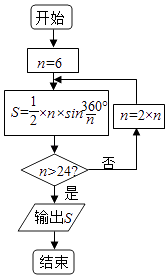
A.2.598
B.3.106
C.3.132
D.3.142
【答案】C
【解析】解:模拟执行程序,可得:
n=6,S=3sin60°= ![]() ,
,
不满足条件n>24,n=12,S=6×sin30°=3,
不满足条件n>24,n=24,S=12×sin15°=12×0.2588=3.1056,
不满足条件n>24,n=48,S=24×sin7.5°=24×0.1305=3.132,
满足条件n>24,退出循环,输出S的值为3.132.
故选:C.
【考点精析】本题主要考查了程序框图的相关知识点,需要掌握程序框图又称流程图,是一种用规定的图形、指向线及文字说明来准确、直观地表示算法的图形;一个程序框图包括以下几部分:表示相应操作的程序框;带箭头的流程线;程序框外必要文字说明才能正确解答此题.


科目:高中数学 来源: 题型:
【题目】已知向量 ![]() =(1,2),
=(1,2), ![]() =(cosα,sinα),设
=(cosα,sinα),设 ![]() =
= ![]() +t
+t ![]() (t为实数).
(t为实数).
(1)若 ![]() ,求当|
,求当| ![]() |取最小值时实数t的值;
|取最小值时实数t的值;
(2)若 ![]() ⊥
⊥ ![]() ,问:是否存在实数t,使得向量
,问:是否存在实数t,使得向量 ![]() ﹣
﹣ ![]() 和向量
和向量 ![]() 的夹角为
的夹角为 ![]() ,若存在,请求出t;若不存在,请说明理由.
,若存在,请求出t;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某同学用“五点法”画函数f(x)=Asin(ωx+φ)+B,A>0,ω>0,|φ|< ![]() 在某一个周期的图象时,列表并填入了部分数据,如表:
在某一个周期的图象时,列表并填入了部分数据,如表:
ωx+φ | 0 |
| π |
| 2π |
x | x1 |
| x2 |
| x3 |
Asin(ωx+φ)+B | 0 |
| 0 | ﹣ | 0 |
(1)请求出上表中的x1 , x2 , x3 , 并直接写出函数f(x)的解析式;
(2)若3sin2 ![]() ﹣
﹣ ![]() mf(
mf( ![]() ﹣
﹣ ![]() )≥m+2对任意x∈[0,2π]恒成立,求实数m的取值范围.
)≥m+2对任意x∈[0,2π]恒成立,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知向量 ![]() =(cosx,﹣1),
=(cosx,﹣1), ![]() =(
=( ![]() sinx,cos2x),设函数f(x)=
sinx,cos2x),设函数f(x)= ![]()
![]() +
+ ![]() .
.
(Ⅰ)求函数f(x)的最小正周期和单调递增区间;
(Ⅱ)当x∈(0, ![]() )时,求函数f(x)的值域.
)时,求函数f(x)的值域.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,半径为1,圆心角为 ![]() 的圆弧
的圆弧 ![]() 上有一点C.
上有一点C. 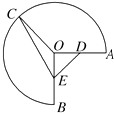
(1)若C为圆弧AB的中点,点D在线段OA上运动,求| ![]() |的最小值;
|的最小值;
(2)若D,E分别为线段OA,OB的中点,当C在圆弧 ![]() 上运动时,求
上运动时,求 ![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】《九章算术》中,将底面为长方形且有一条侧棱与底面垂直的四棱锥称之为阳马,将四个面都为直角三角形的四面体称之为鳖臑,如图,网格纸上正方形小格的边长为1,图中粗线画出的是某几何体毛坯的三视图,第一次切削,将该毛坯得到一个表面积最大的长方体,第二次切削沿长方体的对角面刨开,得到两个三棱柱,第三次切削将两个三棱柱分别沿棱和表面的对角线刨开得到两个鳖臑和两个阳马,则阳马与鳖臑的体积之比为( ) 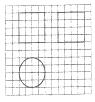
A.3:1
B.2:1
C.1:1
D.1:2
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知等比数列{an}的公比q>1,且a1+a3=20,a2=8. (Ⅰ)求数列{an}的通项公式;
(Ⅱ)设 ![]() ,Sn是数列{bn}的前n项和,对任意正整数n不等式
,Sn是数列{bn}的前n项和,对任意正整数n不等式 ![]() 恒成立,求实数a的取值范围.
恒成立,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】四棱锥P﹣ABCD中,PB⊥底面ABCD,CD⊥PD.底面ABCD为直角梯形,AD∥BC,AB⊥BC,AB=AD=PB=3.点E在棱PA上,且PE=2EA. (Ⅰ)求异面直线PA与CD所成的角;
(Ⅱ)求证:PC∥平面EBD;
(Ⅲ)求二面角A﹣BE﹣D的大小.(用反三角函数表示).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com