
 如图所示的多面体ABCDE中,已知ABCD是边长为2的正方形,平面ABCD⊥平面ABE,∠AEB=90°,AE=BE.
如图所示的多面体ABCDE中,已知ABCD是边长为2的正方形,平面ABCD⊥平面ABE,∠AEB=90°,AE=BE.分析 (I)连结BD,交AC于点N,则点N即为所求,MN∥BE,由线线平行⇒线面平行;
(II)取AB的中点F,连接EF,求出EF,因为平面ABCD⊥平面ABE,交线为EF,证明EF为四棱锥E-ABCD的高,代入棱锥的体积公式计算.
解答 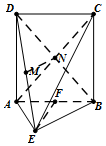 证明:(I)连结BD,交AC于点N,则点N即为所求,
证明:(I)连结BD,交AC于点N,则点N即为所求,
证明如下:
∵ABCD为正方形,
∴N是BD的中点,又M是DE中点,
容易知道MN∥BE,
BE?平面ABE,
MN?平面ABE,
∴MN∥平面ABE
(Ⅱ)取AB的中点F,连接EF
因为△ABE是等腰直角三角形,并且AB=2
所以EF⊥AB,$EF=\frac{1}{2}AB=1$
∵平面ABCD⊥平面ABE,
平面ABCD∩平面ABE=AB,
EF?平面ABE,
∴EF⊥平面ABCD,即EF为四棱锥E-ABCD的高,
∴VE-ABCD=$\frac{1}{3}{S_{ABCD}}•EF$=$\frac{1}{3}×{2^2}×1=\frac{4}{3}$
点评 本题考查了线面平行的证明,考查了棱锥的体积计算,考查了学生的空间想象能力能力与推理论证能力.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 某志愿者到某山区小学支教,为了解留守儿童的幸福感,该志愿者对某班40名学生进行了一次幸福指数的调查问卷,并用茎叶图表示如图(注:图中幸福指数低于70,说明孩子幸福感弱;幸福指数不低于70,说明孩子幸福感强).
某志愿者到某山区小学支教,为了解留守儿童的幸福感,该志愿者对某班40名学生进行了一次幸福指数的调查问卷,并用茎叶图表示如图(注:图中幸福指数低于70,说明孩子幸福感弱;幸福指数不低于70,说明孩子幸福感强).| 幸福感强 | 幸福感弱 | 总计 | |
| 留守儿童 | 6 | 9 | 15 |
| 非留守儿童 | 18 | 7 | 25 |
| 总计 | 24 | 16 | 40 |
| P(K2≥k0) | 0.050 | 0.010 |
| k0 | 3.841 | 6.635 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0 | B. | -3 | C. | 3 | D. | -1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{{\sqrt{3}}}{3}$ | B. | $\sqrt{5}$ | C. | $\sqrt{5}$或$\frac{{\sqrt{10}}}{2}$ | D. | $\frac{{\sqrt{3}}}{3}$或$\frac{{\sqrt{10}}}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | |a|<|b| | B. | $\frac{1}{a}>\frac{1}{b}$ | C. | ${(\frac{1}{2})^a}>{(\frac{1}{2})^b}$ | D. | lna>lnb |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
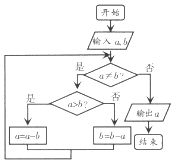 右边程序框图的算法思路源于我国古代数学名著《九章算术》中的“更相减损术”,执行该程序框图,若输入a,b的值分别为16,24,则输出的a的值为( )
右边程序框图的算法思路源于我国古代数学名著《九章算术》中的“更相减损术”,执行该程序框图,若输入a,b的值分别为16,24,则输出的a的值为( )| A. | 2 | B. | 4 | C. | 8 | D. | 16 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com