
【题目】已知f(x)=sin2(2x﹣ ![]() )﹣2tsin(2x﹣
)﹣2tsin(2x﹣ ![]() )+t2﹣6t+1(x∈[
)+t2﹣6t+1(x∈[ ![]() ,
, ![]() ])其最小值为g(t).
])其最小值为g(t).
(1)求g(t)的表达式;
(2)当﹣ ![]() ≤t≤1时,要使关于t的方程g(t)=kt有一个实根,求实数k的取值范围.
≤t≤1时,要使关于t的方程g(t)=kt有一个实根,求实数k的取值范围.
【答案】
(1)解:∵x∈[ ![]() ,
, ![]() ],
],
∴sin(2x﹣ ![]() )∈[﹣
)∈[﹣ ![]() ,1],
,1],
∴f(x)=[sin(2x﹣ ![]() ﹣t]2﹣6t+1,
﹣t]2﹣6t+1,
当t<﹣ ![]() 时,则当sinx=﹣
时,则当sinx=﹣ ![]() 时,f(x)min=
时,f(x)min= ![]() ;
;
当﹣ ![]() ≤t≤1时,当sinx=t时,f(x)min=﹣6t+1;
≤t≤1时,当sinx=t时,f(x)min=﹣6t+1;
当t>1时,当sinx=1时,f(x)min=t2﹣8t+2;
∴g(t)= 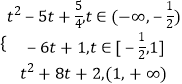
(2)解:当 ![]() 时,g(t)=﹣6t+1.令h(t)=g(t)﹣kt.
时,g(t)=﹣6t+1.令h(t)=g(t)﹣kt.
欲使g(t)=kt有一个实根,则只需使 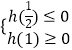 或
或 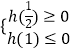 即可.
即可.
解得k≤﹣8或k≥﹣5.
【解析】(1)利用x的范围确定sin(2x﹣ ![]() ),对函数解析式化简整理,对t进行分类讨论,利用抛物线的性质求得每种情况的g(t)的解析式,最后综合.(2)根据(1)中获得当
),对函数解析式化简整理,对t进行分类讨论,利用抛物线的性质求得每种情况的g(t)的解析式,最后综合.(2)根据(1)中获得当 ![]() 时g(t)的解析式,令h(t)=g(t)﹣kt,要使g(t)=kt有一个实根需h(﹣
时g(t)的解析式,令h(t)=g(t)﹣kt,要使g(t)=kt有一个实根需h(﹣ ![]() )和h(1)异号即可.
)和h(1)异号即可.
【考点精析】关于本题考查的三角函数的最值,需要了解函数![]() ,当
,当![]() 时,取得最小值为
时,取得最小值为![]() ;当
;当![]() 时,取得最大值为
时,取得最大值为![]() ,则
,则![]() ,
,![]() ,
,![]() 才能得出正确答案.
才能得出正确答案.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】已知![]() ,
, ![]() ,曲线
,曲线![]() 上的任意一点
上的任意一点![]() 满足:
满足: ![]() .
.
(1)求点![]() 的轨迹方程;
的轨迹方程;
(2)过点![]() 的直线与曲线
的直线与曲线![]() 交于
交于![]() ,
, ![]() 两点,交
两点,交![]() 轴于
轴于![]() 点,设
点,设![]() ,
, ![]() ,试问
,试问![]() 是否为定值?如果是定值,请求出这个定值,如果不是定值,请说明理由.
是否为定值?如果是定值,请求出这个定值,如果不是定值,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某颜料公司生产![]() 两种产品,其中生产每吨
两种产品,其中生产每吨![]() 产品,需要甲染料1吨,乙染料4吨,丙染料2吨,生产每吨
产品,需要甲染料1吨,乙染料4吨,丙染料2吨,生产每吨![]() 产品,需要甲染料1吨,乙染料0吨,丙染料5吨,且该公司一条之内甲、乙、丙三种染料的用量分别不超过50吨,160吨和200吨,如果
产品,需要甲染料1吨,乙染料0吨,丙染料5吨,且该公司一条之内甲、乙、丙三种染料的用量分别不超过50吨,160吨和200吨,如果![]() 产品的利润为300元/吨,
产品的利润为300元/吨, ![]() 产品的利润为200元/吨,则该颜料公司一天之内可获得最大利润为( )
产品的利润为200元/吨,则该颜料公司一天之内可获得最大利润为( )
A. 14000元 B. 16000元 C. 18000元 D. 20000元
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=2sin(2x﹣ ![]() ),x∈R.
),x∈R. 
(1)在给定的平面直角坐标系中,画函数f(x)=2sin(2x﹣ ![]() ),x∈[0,π]的简图;
),x∈[0,π]的简图;
(2)求f(x)=2sin(2x﹣ ![]() ),x∈[﹣π,0]的单调增区间;
),x∈[﹣π,0]的单调增区间;
(3)函数g(x)=2cos2x的图象只经过怎样的平移变换就可得到f(x)=2sin(2x﹣ ![]() ),x∈R的图象?
),x∈R的图象?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com