
【题目】已知椭圆![]() 的离心率为
的离心率为![]() ,左、右焦点分别是
,左、右焦点分别是![]() ,椭圆
,椭圆![]() 上短轴的一个端点与两个焦点构成的三角形的面积为
上短轴的一个端点与两个焦点构成的三角形的面积为![]() ;
;
(1)求椭圆![]() 的方程;
的方程;
(2)过![]() 作垂直于
作垂直于![]() 轴的直线
轴的直线![]() 交椭圆
交椭圆![]() 于
于![]() 两点(点
两点(点![]() 在第二象限),
在第二象限),![]() 是椭圆上位于直线
是椭圆上位于直线![]() 两侧的动点,若
两侧的动点,若![]() ,求证:直线
,求证:直线![]() 的斜率为定值.
的斜率为定值.
科目:高中数学 来源: 题型:
【题目】2019年是中国成立70周年,也是全面建成小康社会的关键之年.为了迎祖国70周年生日,全民齐心奋力建设小康社会,某校特举办“喜迎国庆,共建小康”知识竞赛活动.下面的茎叶图是参赛两组选手答题得分情况,则下列说法正确的是( )
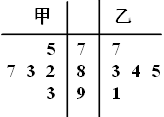
A.甲组选手得分的平均数小于乙组选手的平均数B.甲组选手得分的中位数大于乙组选手的中位数
C.甲组选手得分的中位数等于乙组选手的中位数D.甲组选手得分的方差大于乙组选手的的方差
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在三棱锥P﹣ABC中,PA⊥AB,PA=1,PC=3,BC=2,sin∠PCA![]() ,E,F,G分别为线段的PC,PB,AB中点,且BE
,E,F,G分别为线段的PC,PB,AB中点,且BE![]() .
.
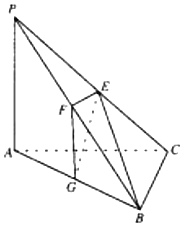
(1)求证:AB⊥BC;
(2)若M为线段BC上一点,求三棱锥M﹣EFG的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() ,
, ![]() 满足约束条件
满足约束条件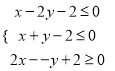 ,若
,若![]() 取得最大值的最优解不唯一,则实数
取得最大值的最优解不唯一,则实数![]() 的值为__________.
的值为__________.
【答案】![]() 或
或![]()
【解析】由题可知若![]() 取得最大值的最优解不唯一则
取得最大值的最优解不唯一则![]() 必平行于可行域的某一边界,如图:
必平行于可行域的某一边界,如图: 要Z最大则直线与y轴的截距最大即可,当a<0时,则平行AC直线即可故a=-2,当a>0时,则直线平行AB即可,故a=1
要Z最大则直线与y轴的截距最大即可,当a<0时,则平行AC直线即可故a=-2,当a>0时,则直线平行AB即可,故a=1
点睛:线性规划为常考题型,解决此题务必要理解最优解个数为无数个时的条件是什么,然后根据几何关系求解即可
【题型】填空题
【结束】
16
【题目】《数书九章》三斜求积术:“以小斜幂,并大斜幂,减中斜幂,余半之,自乘于上;以小斜幂乘大斜幂,减上,余四约一,为实,一为从隅,开平方得积”.秦九韶把三角形的三条边分别称为小斜、中斜和大斜,“术”即方法.以![]() ,
, ![]() ,
, ![]() ,
, ![]() 分别表示三角形的面积,大斜,中斜,小斜;
分别表示三角形的面积,大斜,中斜,小斜; ![]() ,
, ![]() ,
, ![]() 分别为对应的大斜,中斜,小斜上的高;则
分别为对应的大斜,中斜,小斜上的高;则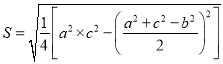
![]()
![]() .若在
.若在![]() 中
中![]() ,
, ![]() ,
, ![]() ,根据上述公式,可以推出该三角形外接圆的半径为__________.
,根据上述公式,可以推出该三角形外接圆的半径为__________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】给出以下四个结论:
(1)函数![]() 的对称中心是
的对称中心是![]() ;
;
(2)若关于![]() 的方程
的方程![]() 在
在![]() 没有实数根,则
没有实数根,则![]() 的取值范围是
的取值范围是![]() ;
;
(3)已知点![]() 与点
与点![]() 在直线
在直线![]() 两侧,则
两侧,则![]() ;
;
(4)若将函数![]() 的图象向右平移
的图象向右平移![]() 个单位后变为偶函数,则
个单位后变为偶函数,则![]() 的最小值是
的最小值是![]() ;
;
其中正确的结论是:_____________________(把所有正确命题的序号填上).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,我市某居民小区拟在边长为1百米的正方形地块![]() 上划出一个三角形地块
上划出一个三角形地块![]() 种植草坪,两个三角形地块
种植草坪,两个三角形地块![]() 与
与![]() 种植花卉,一个三角形地块
种植花卉,一个三角形地块![]() 设计成水景喷泉,四周铺设小路供居民平时休闲散步,点
设计成水景喷泉,四周铺设小路供居民平时休闲散步,点![]() 在边
在边![]() 上,点
上,点![]() 在边
在边![]() 上,记
上,记![]() .
.
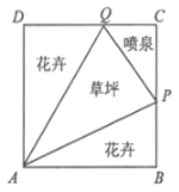
(1)当![]() 时,求花卉种植面积
时,求花卉种植面积![]() 关于
关于![]() 的函数表达式,并求
的函数表达式,并求![]() 的最小值;
的最小值;
(2)考虑到小区道路的整体规划,要求![]() ,请探究
,请探究![]() 是否为定值,若是,求出此定值,若不是,请说明理由.
是否为定值,若是,求出此定值,若不是,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,曲线C的参数为![]() (α为参数),以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,直线l的极坐标方程为
(α为参数),以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,直线l的极坐标方程为![]() ;
;
(1)写出曲线C的普通方程和直线l的参数方程;
(2)设点P(m,0),若直线l与曲线C相交于A,B两点,且|PA|![]() |PB|=1,求实数m的值.
|PB|=1,求实数m的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com