
| A. | 1-2a | B. | 2a-1 | C. | ($\frac{1}{2}$)a-1 | D. | 1-($\frac{1}{2}$)a |
分析 利用奇函数得出f(x)$\left\{\begin{array}{l}{-lo{g}_{\frac{1}{2}}(1-x),x∈(-1,0)}\\{-1+|x+3|,x∈(-∞,-1]}\end{array}\right.$,并画出图象,根据对称性得出x1+x2+x3+x4+x5=x3,再求出x3=1-2a即可.
解答 解:∵f(x)=$\left\{\begin{array}{l}{lo{g}_{\frac{1}{2}}(x+1),x∈[0,1)}\\{1-|x-3|,x∈[1,+∞)}\end{array}\right.$,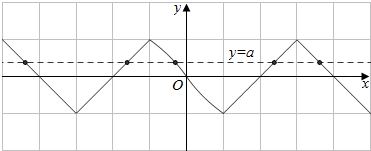
且f(x)为奇函数,
∴当x∈(-∞,0)时,
f(x)=$\left\{\begin{array}{l}{-lo{g}_{\frac{1}{2}}(1-x),x∈(-1,0)}\\{-1+|x+3|,x∈(-∞,-1]}\end{array}\right.$,
当a∈(0,1),方程f(x)=a有5个根,(如图)
从小到到依次设为:x1,x2,x3,x4,x5,
显然,x1与x2关于x=-3轴对称,x4,x5关于x=3对称,
即x1+x2=-6,x4+x5=6,
因此,所有实根之和为:x1+x2+x3+x4+x5=x3,
而x3∈(-1,0),故令-$lo{g}_{\frac{1}{2}}(1-x)$=a,
解得x3=1-2a,即x1+x2+x3+x4+x5=1-2a,
故答案为:A.
点评 本题主要函数的图象与性质,涉及函数的奇偶性和图象变换,并运用图象的对称性处理数量关系,体现了数形结合的解题思想,属于中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 组号 | 分组 | 回答正确的人数 | 回答正确的人数占本组的频率 | 频率分布直方图 |
| 第1组 | [15,25) | 5 | 0.5 | 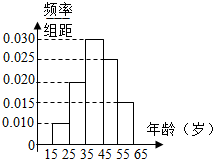 |
| 第2组 | [25,35) | a | 0.9 | |
| 第3组 | [35,45) | 27 | x | |
| 第4组 | [45,55) | 9 | 0.36 | |
| 第5组 | [55,65] | 3 | 0.2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com