
我们称离心率![]() 的椭圆叫做“黄金椭圆”,若
的椭圆叫做“黄金椭圆”,若![]() 为黄金椭圆,以下四个命题:
为黄金椭圆,以下四个命题:
(1)长半轴长a,短半轴长b,半焦距c成等比数列.
(2)一个长轴顶点与其不同侧的焦点以及一个短轴顶点构成直角三角形.
(3)以两条通经的4个端点为顶点的四边形为正方形.
(4)P、Q为椭圆上任意两点,M为PQ中点,只要PQ与OM的斜率存在,必有kpQ·kOM的定值.
其中正确命题的序号为________.
 新课标同步训练系列答案
新课标同步训练系列答案 一线名师口算应用题天天练一本全系列答案
一线名师口算应用题天天练一本全系列答案 小学学习好帮手系列答案
小学学习好帮手系列答案科目:高中数学 来源: 题型:
| ||
| 2 |
| x2 |
| a2 |
| y2 |
| b2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
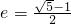 的椭圆叫做“黄金椭圆”,若
的椭圆叫做“黄金椭圆”,若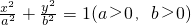 为黄金椭圆,以下四个命题:
为黄金椭圆,以下四个命题:查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
| ||
| 2 |
| x2 |
| a2 |
| y2 |
| b2 |
查看答案和解析>>
科目:高中数学 来源:2012-2013学年湖南省郴州市安仁一中高三(上)月考数学试卷(文科)(解析版) 题型:填空题
 的椭圆叫做“黄金椭圆”,若
的椭圆叫做“黄金椭圆”,若 为黄金椭圆,以下四个命题:
为黄金椭圆,以下四个命题:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com