
【题目】在直角坐标系xOy中,直线l的参数方程为  (t为参数),在以坐标原点O为极点,x轴的正半轴为极轴的极坐标系中,曲线C的极坐标方程为ρ=2
(t为参数),在以坐标原点O为极点,x轴的正半轴为极轴的极坐标系中,曲线C的极坐标方程为ρ=2 ![]() cos(
cos( ![]() +θ).
+θ).
(I)求直线l的普通方程和曲线C的直角坐标方程;
(Ⅱ)设直线l与曲线C相交于M,N两点,求|MN|的值.
【答案】解:(Ⅰ)∵直线l的参数方程为 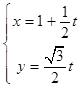 (t为参数),
(t为参数),
∴消去参数t,得直线l的直角坐标方程为 ![]() =0.
=0.
∵曲线C的极坐标方程为ρ=2 ![]() cos(
cos( ![]() +θ).
+θ).
即 ![]() =2cosθ﹣2sinθ,
=2cosθ﹣2sinθ,
即ρ2=2ρcosθ﹣2ρsinθ,
∴曲线C的直角坐标方程为x2+y2=2x﹣2y,即(x﹣1)2+(y+1)2=2.
(Ⅱ)曲线C是以C(1,﹣1)为圆心,以r= ![]() 为半径的圆,
为半径的圆,
圆心C(1,﹣1)到直线l的距离d= 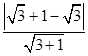 =
= ![]() ,
,
∵直线l与曲线C相交于M,N两点,
∴|MN|=2 ![]() =2
=2 ![]() =
= ![]()
【解析】(Ⅰ)直线l的参数方程消去参数t,得直线l的直角坐标方程为 ![]() =0;曲线C的极坐标方程l转化为ρ2=2ρcosθ﹣2ρsinθ,由此能求出曲线C的直角坐标方程.(Ⅱ)曲线C是以C(1,﹣1)为圆心,以r=
=0;曲线C的极坐标方程l转化为ρ2=2ρcosθ﹣2ρsinθ,由此能求出曲线C的直角坐标方程.(Ⅱ)曲线C是以C(1,﹣1)为圆心,以r= ![]() 为半径的圆,求出圆心C(1,﹣1)到直线l的距离d,由|MN|=2
为半径的圆,求出圆心C(1,﹣1)到直线l的距离d,由|MN|=2 ![]() ,能求出结果.
,能求出结果.


 优学名师名题系列答案
优学名师名题系列答案科目:高中数学 来源: 题型:
【题目】如图,四棱锥S﹣ABCD中,底面ABCD为直角梯形,AB∥CD,BC⊥CD,平面SCD⊥平面ABCD,SC=SD=CD=AD=2AB,M,N分别为SA,SB的中点,E为CD中点,过M,N作平面MNPQ分别与BC,AD交于点P,Q,若 ![]() =t
=t ![]() .
. 
(1)当t= ![]() 时,求证:平面SAE⊥平面MNPQ;
时,求证:平面SAE⊥平面MNPQ;
(2)是否存在实数t,使得二面角M﹣PQ﹣A的平面角的余弦值为 ![]() ?若存在,求出实数t的值;若不存在,说明理由.
?若存在,求出实数t的值;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在三棱柱ABC﹣A1B1C1中,AA1⊥平面ABC,AB=BC=CA=2![]() ,AA1=4,D为A1B1的中点,E为棱BB1上的点,AB1⊥平面C1DE,且B1,C1,D,E四点在同一球面上,则该球的表面积为( )
,AA1=4,D为A1B1的中点,E为棱BB1上的点,AB1⊥平面C1DE,且B1,C1,D,E四点在同一球面上,则该球的表面积为( )
A. 9π B. 11π C. 12π D. 14π
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在如图所示的几何体中,四边形ABCD是菱形,ADNM是矩形,平面ADNM⊥平面ABCD,∠DAB=60°,AD=2,AM=1,E为AB的中点.
(Ⅰ)求证:AN∥平面MEC;
(Ⅱ)在线段AM上是否存在点P,使二面角P﹣EC﹣D的大小为 ![]() ?若存在,求出AP的长h;若不存在,请说明理由.
?若存在,求出AP的长h;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=x3+ax2+bx+a2在x=1处有极值4.
(I)求实数a,b的值;
(Ⅱ)当a>0时,求曲线y=f(x)在点(﹣2,f(﹣2))处的切线方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】将参加冬季越野跑的600名选手编号为:001,002,…,600.采用系统抽样方法抽取一个容量为50的样本,把编号分50组后,在第一组的001到012这12个编号中随机抽得的号码为004.这600名选手分穿着三种颜色的衣服,从001到301穿红色衣服,从302到496穿白色衣服,从497到600穿黄色衣服.则抽到穿白色衣服的选手人数为 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系xOy中,圆C的参数方程 ![]() 为参数),以O为极点,x轴的非负半轴为极轴建立极坐标系.
为参数),以O为极点,x轴的非负半轴为极轴建立极坐标系.
(1)求圆C的极坐标方程;
(2)直线l的极坐标方程是 ![]() ,射线
,射线 ![]() 与圆C的交点为O,P,与直线l的交点为Q,求|OP||OQ|的范围.
与圆C的交点为O,P,与直线l的交点为Q,求|OP||OQ|的范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知f(x)是定义在R上的偶函数,且f(x+2)=f(x)对x∈R恒成立,当x∈[0,1]时,f(x)=2x , 则 ![]() =( )
=( )
A.![]()
B.![]()
C.![]()
D.1
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,以坐标原点为圆心且与直线mx﹣y﹣2m+1=0(m∈R)相切的所有圆中,半径最大的圆的标准方程为( )
A.x2+y2=5
B.x2+y2=3
C.x2+y2=9
D.x2+y2=7
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com