
| 1 | 9 |
| 1 |
| 9 |
| 1 |
| 9 |
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
| 3 |
| 8 |
| 27 |
| C | 2 3 |
| 2 |
| 3 |
| 1 |
| 3 |
| 8 |
| 27 |
| C | 2 4 |
| 2 |
| 3 |
| 1 |
| 3 |
| 16 |
| 81 |
| 8 |
| 27 |
| 8 |
| 27 |
| 16 |
| 81 |
| 64 |
| 81 |
| 64 |
| 81 |
| C | 2 3 |
| 2 |
| 3 |
| 1 |
| 3 |
| C | 2 3 |
| 1 |
| 3 |
| 2 |
| 3 |
| 1 |
| 3 |
| 10 |
| 27 |
| C | 2 4 |
| 2 |
| 3 |
| 1 |
| 3 |
| 8 |
| 27 |
| 8 |
| 27 |
| 10 |
| 27 |
| 1 |
| 3 |
| 1 |
| 3 |
| 10 |
| 27 |
| 8 |
| 27 |
| 107 |
| 27 |


科目:高中数学 来源: 题型:解答题
 (已知甲回答每个问题的正确率相同,且相互之间没有影响)
(已知甲回答每个问题的正确率相同,且相互之间没有影响)查看答案和解析>>
科目:高中数学 来源:2011年甘肃省天水一中高考数学四模试卷(理科)(解析版) 题型:解答题
 (已知甲回答每个问题的正确率相同,且相互之间没有影响)
(已知甲回答每个问题的正确率相同,且相互之间没有影响)查看答案和解析>>
科目:高中数学 来源:2008-2009学年浙江省宁波市十校高三联考数学试卷(理科)(解析版) 题型:解答题
 (已知甲回答每个问题的正确率相同,且相互之间没有影响)
(已知甲回答每个问题的正确率相同,且相互之间没有影响)查看答案和解析>>
科目:高中数学 来源:安徽省2010届高三第三次质检(理) 题型:解答题
某地区举行环保知识大赛,比赛分初赛和决赛两部分,初赛采用选用选一题答一题的方式进行,每位选手最多有5次选题答题的机会,选手累计答对3题或答错3题即终止其初赛的比赛,答对3题直接进入决赛,答错3次者则被淘汰,已知选手甲连续两次
答错的概率为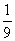 (已知甲回答每个问题的正确率相同,且相互之间没有影响)
(已知甲回答每个问题的正确率相同,且相互之间没有影响)
(I)求甲选手回答一个问题的正确率;
(II)求选手甲进入决赛的概率;
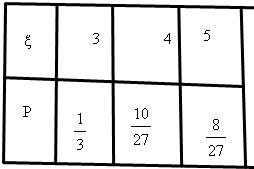
(III)设选手甲在初赛中的答题的个数为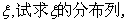 并求出
并求出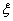 的数学期望。
的数学期望。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com