
【题目】已知函数![]() .
.
(1)解关于x的不等式![]() ;
;
(2)对任意的![]() (﹣1,2),
(﹣1,2),![]() 恒成立,求实数k的取值范围.
恒成立,求实数k的取值范围.
【答案】:(1)当![]() 时,解集为
时,解集为![]() ,当
,当![]() 时,解集为
时,解集为![]() . 当
. 当![]() 时,解集为
时,解集为![]() .(2)
.(2)![]()
【解析】
(1)按照k与﹣1的大小分三种情况讨论;(2)分离参数k后,构造函数,利用基本不等式求得最小值即可.
(1)因为f(x)<2,
∴x2+(1﹣k)x﹣k<0,
∴(x+1)(x﹣k)<0
当k>﹣1时,﹣1<x<k,
当k=﹣1时,不等式无解,
当k<﹣1时,k<x<﹣1,
综上所述:当k>﹣1时,不等式的解集为(﹣1,k);
当k=﹣1时,不等式无解;
当k<﹣1时,不等式的解集为(k,﹣1);
(2)对任意的x∈(﹣1,2),f(x)≥1k≤![]() =x+1+
=x+1+![]() ﹣1恒成立,
﹣1恒成立,
令g(x)=x+1+![]() ﹣1,x∈(﹣1,2),则k≤g(x)min
﹣1,x∈(﹣1,2),则k≤g(x)min
∵g(x)≥2![]() ﹣1=1,即g(x)min=1,
﹣1=1,即g(x)min=1,
故k≤1.


 鸿图图书寒假作业假期作业吉林大学出版社系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案科目:高中数学 来源: 题型:
【题目】如果函数![]() 在定义域的某个区间
在定义域的某个区间![]() 上的值域恰为
上的值域恰为![]() ,则称函数
,则称函数![]() 为
为![]() 上的等域函数,
上的等域函数,![]() 称为函数
称为函数![]() 的一个等域区间.
的一个等域区间.
(1)若函数![]() ,
,![]() ,则函数
,则函数![]() 存在等域区间吗?若存在,试写出其一个等域区间,若不存在,说明理由
存在等域区间吗?若存在,试写出其一个等域区间,若不存在,说明理由
(2)已知函数![]() ,其中
,其中![]() 且
且![]() ,
,![]() ,
,![]() .
.
(ⅰ)当![]() 时,若函数
时,若函数![]() 是
是![]() 上的等域函数,求
上的等域函数,求![]() 的解析式;
的解析式;
(ⅱ)证明:当![]() ,
,![]() 时,函数
时,函数![]() 不存在等域区间.
不存在等域区间.
查看答案和解析>>
科目:高中数学 来源: 题型:
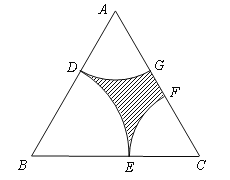
【题目】近年来,随着我市经济的快速发展,政府对民生越来越关注市区现有一块近似正三角形的土地![]() (如图所示),其边长为2百米,为了满足市民的休闲需求,市政府拟在三个顶点处分别修建扇形广场,即扇形
(如图所示),其边长为2百米,为了满足市民的休闲需求,市政府拟在三个顶点处分别修建扇形广场,即扇形![]() 和
和![]() ,其中
,其中![]() 与
与![]() 、
、![]() 分别相切于点
分别相切于点![]() ,且
,且![]() 与
与![]() 无重叠,剩余部分(阴影部分)种植草坪.设
无重叠,剩余部分(阴影部分)种植草坪.设![]() 长为
长为![]() (单位:百米),草坪面积为
(单位:百米),草坪面积为![]() (单位:万平方米).
(单位:万平方米).
(1)试用![]() 分别表示扇形
分别表示扇形![]() 和
和![]() 的面积,并写出
的面积,并写出![]() 的取值范围;
的取值范围;
(2)当![]() 为何值时,草坪面积最大?并求出最大面积.
为何值时,草坪面积最大?并求出最大面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知M,N是焦点为F的抛物线y2=2px(p>0)上两个不同的点,线段MN的中点A的横坐标为![]() .
.
(1)求|MF|+|NF|的值;
(2)若p=2,直线MN与x轴交于点B,求点B的横坐标的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设三棱锥![]() 的底面是正三角形,侧棱长均相等,
的底面是正三角形,侧棱长均相等,![]() 是棱
是棱![]() 上的点(不含端点),记直线
上的点(不含端点),记直线![]() 与直线
与直线![]() 所成角为
所成角为![]() ,直线
,直线![]() 与平面
与平面![]() 所成角为
所成角为![]() ,二面角
,二面角![]() 的平面角为
的平面角为![]() ,则( )
,则( )
A. ![]() B.
B. ![]()
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥![]() 中,
中,![]() 平面ABCD,底部ABCD为菱形,E为CD的中点.
平面ABCD,底部ABCD为菱形,E为CD的中点.

(Ⅰ)求证:BD⊥平面PAC;
(Ⅱ)若∠ABC=60°,求证:平面PAB⊥平面PAE;
(Ⅲ)棱PB上是否存在点F,使得CF∥平面PAE?说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图是一几何体的平面展开图,其中四边形![]() 为正方形,
为正方形,![]() 分别为
分别为![]() 的中点.在此几何体中,给出下列结论,其中正确的结论是( )
的中点.在此几何体中,给出下列结论,其中正确的结论是( )

A.平面![]() 平面
平面![]() B.直线
B.直线![]() 平面
平面![]()
C.直线![]() 平面
平面![]() D.直线
D.直线![]() 平面
平面![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,直三棱柱ABCA1B1C1中(侧棱与底面垂直的棱柱),AC=BC=1,∠ACB=90°,AA1=![]() ,D 是A1B1的中点.
,D 是A1B1的中点.

(1)求证:C1D⊥平面AA1B1B;
(2)当点F 在BB1上的什么位置时,AB1⊥平面C1DF ?并证明你的结论.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com