
【题目】定义在R上的函数f(x),f(0)≠0,f(1)=2,当x>0,f(x)>1,且对任意a,b∈R,有f(a+b)=f(a)f(b).
(1)求证:对任意x∈R,都有f(x)>0;
(2)判断f(x)在R上的单调性,并用定义证明;
(3)求不等式f(3﹣2x)>4的解集.
【答案】
(1)证明:令a=b=0,
则f(0)=f(0)f(0),又f(0)≠0,∴f(0)=1,
当x<0时,﹣x>0,∴f(﹣x)>1,
∵f(0)=f(x)f(﹣x)=1,
∴f(x)= ![]() ,
,
∵f(﹣x)>1,∴0< ![]() <1,即0<f(x)<1,
<1,即0<f(x)<1,
又当x>0,f(x)>1; 且f(0)=1,
所以对任意x∈R,都有f(x)>0
(2)解:f(x)在R上是增函数,
证明如下:设x1<x2,
则f(x2)=f(x2﹣x1+x1)=f(x2﹣x1)f(x1),
∵x2﹣x1>0,∴f(x2﹣x1)>1,又f(x1)>0,
∴f(x2﹣x1)f(x1)>f(x1),
即f(x2)>f(x1),
∴f(x)在R上是增函数
(3)解:∵f(2)=f(1)f(1)=4,
∴f(3﹣2x)>4f(3﹣2x)>f(2),
∵f(x)在R上是增函数,
∴3﹣2x>2,
解得x< ![]() .
.
∴不等式f(3﹣2x)>4的解集为(﹣∞, ![]() )
)
【解析】(1)先令a=b=0计算f(0)=1,当x<0时,f(x)= ![]() >0,从而得出结论;(2)设x1<x2 , 则f(x2)=f(x2﹣x1+x1)=f(x2﹣x1)f(x1)>f(x1),于是f(x)在R上是增函数;(3)f(2)=4,利用函数的单调性得出3﹣2x>2,解出答案.
>0,从而得出结论;(2)设x1<x2 , 则f(x2)=f(x2﹣x1+x1)=f(x2﹣x1)f(x1)>f(x1),于是f(x)在R上是增函数;(3)f(2)=4,利用函数的单调性得出3﹣2x>2,解出答案.


 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案科目:高中数学 来源: 题型:
【题目】某种商品在近30天内每件的销售价格P(元)与时间t(天)的函数关系式近似满足P= ![]() ,商品的日销售量Q(件)与时间t(天)的函数关系式近似满足Q=﹣t+40(1≤t≤30,t∈N).
,商品的日销售量Q(件)与时间t(天)的函数关系式近似满足Q=﹣t+40(1≤t≤30,t∈N).
(1)求这种商品日销售金额y与时间t的函数关系式;
(2)求y的最大值,并指出日销售金额最大的一天是30天中第几天.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲、乙、丙三名学生参加某电视台举办的国学知识竞赛,在本次竞赛中只有过关和不过关两种结果,假设甲、乙、丙竞赛过关的概率分别为![]() ,且他们竞赛过关与否互不影响.
,且他们竞赛过关与否互不影响.
(1)求在这次国学知识竞赛中,甲、乙、丙三名学生至少有一名学生过关的概率;
(2)记在这次国学知识竞赛中,甲、乙、丙三名学生过关的人数为![]() ,求随机变量
,求随机变量![]() 的分布列和数学期望
的分布列和数学期望![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某种水果的单个质量在500g以上视为特等品.随机抽取1000个该水果,结果有50个特等品.将这50个水果的质量数据分组,得到下边的频率分布表.
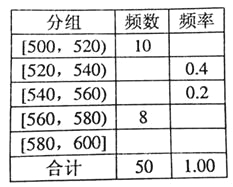
(1)估计该水果的质量不少于560g的概率;
(2)若在某批水果的检测中,发现有15个特等品,据此估计该批水果中没有达到特等品的个数.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知全集U=R,集合A={x|x<﹣4,或x>2},B={x|﹣1≤2x﹣1﹣2≤6}.
(1)求A∩B、(UA)∪(UB);
(2)若集合M={x|2k﹣1≤x≤2k+1}是集合A的子集,求实数k的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在某大学自主招生考试中,所有选报Ⅱ类志向的考生全部参加了“数学与逻辑”和“阅读与表达”两个科目的考试,成绩分为A,B,C,D,E五个等级.某考场考生的两科考试成绩的数据统计如下图所示,其中“数学与逻辑”科目的成绩等级为B的考生有10人.
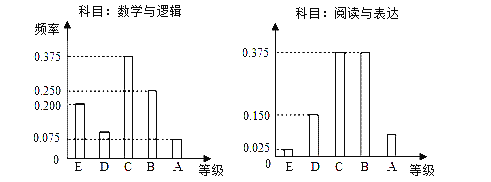
(1)求该考场考生中“阅读与表达”科目中成绩等级为A的人数;
(2)已知参加本考场测试的考生中,恰有2人的两科成绩等级均为A.在至少一科成绩等级为A的考生中,随机抽取2人进行访谈,求这2人的两科成绩等级均为A的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() (
(![]() 为常数,
为常数,![]() 是自然对数的底数),曲线
是自然对数的底数),曲线![]() 在点
在点![]() 处的切线与
处的切线与![]() 轴平行.
轴平行.
(1)求![]() 的值;
的值;
(2)求![]() 的单调区间;
的单调区间;
(3)设![]() ,其中
,其中![]() 为
为![]() 的导函数.证明:对任意
的导函数.证明:对任意![]() ,
,![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com