
【题目】已知函数![]() ,
,![]() ,且
,且![]() 点
点![]() 处取得极值.
处取得极值.
(Ⅰ)若关于![]() 的方程
的方程![]() 在区间
在区间![]() 上有解,求
上有解,求![]() 的取值范围;
的取值范围;
(Ⅱ)证明:![]() .
.
【答案】(Ⅰ)![]() ;(Ⅱ)证明见解析.
;(Ⅱ)证明见解析.
【解析】
试题(Ⅰ)求导,利用![]() 求
求![]() 值;分离常数,构造函数,转化为求函数的值域问题;(Ⅱ)作差构造函数,将证明不等式恒成立问题转化为求函数的最值问题.
值;分离常数,构造函数,转化为求函数的值域问题;(Ⅱ)作差构造函数,将证明不等式恒成立问题转化为求函数的最值问题.
试题解析:解:(Ⅰ)∵![]() , ∴
, ∴![]()
∵函数![]() 在点
在点![]() 处取得极值,
处取得极值,
∴![]() ,即当
,即当![]() 时
时![]() ,
,
∴![]() ,则得
,则得![]() .经检验符合题意 2分
.经检验符合题意 2分
∵![]() ,∴
,∴![]() , ∴
, ∴![]() .
.
令![]() , 则
, 则![]() .
.
∴当![]() 时,
时,![]() 随
随![]() 的变化情况表:
的变化情况表:
| 1 | (1,2) | 2 | (2,3) | 3 |
| + | 0 | - | ||
| ↗ | 极大值 | ↘ |
计算得:![]() ,
,![]() ,
,![]() ,
,![]()
所以![]() 的取值范围为
的取值范围为![]() . 6分
. 6分
(Ⅱ)证明:令![]()
![]()
![]() ,
,
则![]()
![]() ,
,
令![]() ,则
,则![]() ,
,
![]() 函数
函数![]() 在
在![]() 递增,
递增,![]() 在
在![]() 上的零点最多一个
上的零点最多一个
又![]()
![]() ,
,![]() ,
,![]() 存在唯一的
存在唯一的![]() 使得
使得![]() , 9分
, 9分
且当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() .
.
即当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() .
.
![]()
![]() 在
在![]() 递减,在
递减,在![]() 递增,从而
递增,从而![]()
![]() .
.
由![]() 得
得![]() 即
即![]() ,两边取对数得:
,两边取对数得:![]() ,
,![]()
![]() ,
,
![]()
![]() ,从而证得
,从而证得![]() . 12分
. 12分


科目:高中数学 来源: 题型:
【题目】将正方形![]() 沿对角线
沿对角线![]() 折成直二面角
折成直二面角![]() ,有如下四个结论:
,有如下四个结论:
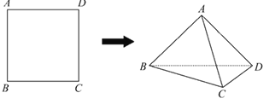
(1)![]() ;(2)
;(2)![]() 是等边三角形;
是等边三角形;
(3)![]() 与平面
与平面![]() 所成的角为60°;(4)
所成的角为60°;(4)![]() 与
与![]() 所成的角为
所成的角为![]() .
.
其中错误的结论是( )
A.(1)B.(2)C.(3)D.(4)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知两个分类变量X和Y,由他们的观测数据计算得到K2的观测值范围是3.841<k<6.635,据K2的临界值表,则以下判断正确的是( )
![]()
P(K2≥k) | 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.01 | 0.005 | 0.001 |
k | 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
A.在犯错误概率不超过0.05的前提下,认为变量X与Y有关系
B.在犯错误概率不超过0.05的前提下,认为变量X与Y没有关系
C.在犯错误概率不超过0.01的前提下,认为变量X与Y有关系
D.在犯错误概率不超过0.01的前提下,认为变量X与Y没有关系
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,三棱柱![]() 中,
中,![]() 侧面
侧面![]() ,已知
,已知![]() ,
,![]() ,
,![]() ,点E是棱
,点E是棱![]() 的中点.
的中点.

(1)求证:![]() 平面ABC;
平面ABC;
(2)在棱CA上是否存在一点M,使得EM与平面![]() 所成角的正弦值为
所成角的正弦值为![]() ,若存在,求出
,若存在,求出![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】学校艺术节对![]() 四件参赛作品只评一件一等奖,在评奖揭晓前,甲,乙,丙,丁四位同学对这四件参赛作品预测如下:
四件参赛作品只评一件一等奖,在评奖揭晓前,甲,乙,丙,丁四位同学对这四件参赛作品预测如下:
甲说:“是![]() 或
或![]() 作品获得一等奖”; 乙说:“
作品获得一等奖”; 乙说:“ ![]() 作品获得一等奖”;
作品获得一等奖”;
丙说:“ ![]() 两件作品未获得一等奖”; 丁说:“是
两件作品未获得一等奖”; 丁说:“是![]() 作品获得一等奖”.
作品获得一等奖”.
评奖揭晓后,发现这四位同学中只有两位说的话是对的,则获得一等奖的作品是_________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在某公司举行的一次真假游戏的有奖竞猜中,设置了“科技”和“生活”这两类试题,规定每位职工最多竞猜3次,每次竞猜的结果相互独立.猜中一道“科技”类试题得4分,猜中一道“生活”类试题得2分,两类试题猜不中的都得0分.将职工得分逐次累加并用X表示,如果X的值不低于4分就认为通过游戏的竞猜,立即停止竞猜,否则继续竞猜,直到竞猜完3次为止.竞猜的方案有以下两种:方案1:先猜一道“科技”类试题,然后再连猜两道“生活”类试题;
方案2:连猜三道“生活”类试题.
设职工甲猜中一道“科技”类试题的概率为0.5,猜中一道“生活”类试题的概率为0.6.
(1)你认为职工甲选择哪种方案通过竞猜的可能性大?并说明理由.
(2)职工甲选择哪一种方案所得平均分高?并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】中国古代儒家要求学生掌握六种基本才能:礼乐射御书数,某校国学社团周末开展“六艺”课程讲座活动,每天连排六节,每艺一节,排课有如下要求:“礼”和“数”不能相邻,“射”和“乐”必须相邻,则“六艺”课程讲座不同的排课顺序共有( )
A.24种B.72种C.96种D.144种
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】中医药,是包括汉族和少数民族医药在内的我国各民族医药的统称,是反映中华民族对生命、健康和疾病的认识,具有悠久历史传统和独特理论及技术方法的医药学体系,是中华民族的瑰宝.某科研机构研究发现,某品种中医药的药物成分甲的含量![]() (单位:克)与药物功效
(单位:克)与药物功效![]() (单位:药物单位)之间具有关系
(单位:药物单位)之间具有关系![]() .检测这种药品一个批次的5个样本,得到成分甲的平均值为4克,标准差为
.检测这种药品一个批次的5个样本,得到成分甲的平均值为4克,标准差为![]() 克,则估计这批中医药的药物功效的平均值为( )
克,则估计这批中医药的药物功效的平均值为( )
A.22药物单位B.20药物单位C.12药物单位D.10药物单位
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com