
【题目】某小学举办“父母养育我,我报父母恩”的活动,对六个年级(一年级到六年级的年级代码分别为1,2…,6)的学生给父母洗脚的百分比y%进行了调查统计,绘制得到下面的散点图.
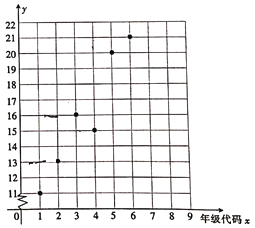
(1)由散点图看出,可用线性回归模型拟合y与x的关系,请用相关系数加以说明;
(2)建立y关于x的回归方程,并据此预计该校学生升入中学的第一年(年级代码为7)给父母洗脚的百分比.
附注:参考数据:![]()
参考公式:相关系数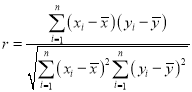 ,若r>0.95,则y与x的线性相关程度相当高,可用线性回归模型拟合y与x的关系.回归方程
,若r>0.95,则y与x的线性相关程度相当高,可用线性回归模型拟合y与x的关系.回归方程![]() 中斜率与截距的最小二乘估计公式分别为
中斜率与截距的最小二乘估计公式分别为![]() =
=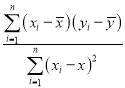 ,
,![]() .
.
科目:高中数学 来源: 题型:
【题目】下列四个命题中真命题是![]()
![]()
A. 同垂直于一直线的两条直线互相平行
B. 底面各边相等,侧面都是矩形的四棱柱是正四棱柱
C. 过空间任一点与两条异面直线都垂直的直线有且只有一条
D. 过球面上任意两点的大圆有且只有一个
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,四棱锥![]() 的底面是边长为1的正方形,侧棱
的底面是边长为1的正方形,侧棱![]() 底面
底面![]() ,且
,且![]() ,
,![]() 是侧棱
是侧棱![]() 上的动点.
上的动点.
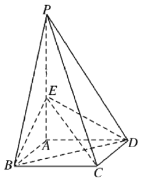
(1)求四棱锥![]() 的体积;
的体积;
(2)如果![]() 是
是![]() 的中点,求证:
的中点,求证:![]() 平面
平面![]() ;
;
(3)不论点![]() 在侧棱
在侧棱![]() 的任何位置,是否都有
的任何位置,是否都有![]() ?证明你的结论.
?证明你的结论.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知直线![]() 与圆锥曲线C相交于A,B两点,与
与圆锥曲线C相交于A,B两点,与![]() 轴、
轴、![]() 轴分别交于D、E两点,且满足
轴分别交于D、E两点,且满足![]() .
.
(1)已知直线![]() 的方程为
的方程为![]() ,且A的横坐标小于B的横坐标,抛物线C的方程为
,且A的横坐标小于B的横坐标,抛物线C的方程为![]() ,求
,求![]() 的值;
的值;
(2)已知双曲线![]() ,求点D的坐标.
,求点D的坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设![]() ,
,![]() 是两条不同的直线,
是两条不同的直线,![]() ,
,![]() ,
,![]() 是三个不同的平面,给出下列四个命题:
是三个不同的平面,给出下列四个命题:
①若![]() ,
,![]() ,则
,则![]()
②若![]() ,
,![]() ,
,![]() ,则
,则![]()
③若![]() ,
,![]() ,则
,则![]()
④若![]() ,
,![]() ,则
,则![]()
其中正确命题的序号是( )
A.①和②B.②和③C.③和④D.①和④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了对某课题进行研究,用分层抽样方法从三所高校A,B,C的相关人员中,抽取若干人组成研究小组、有关数据见下表(单位:人)
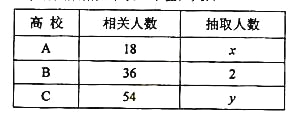
(I) 求x,y ;
(II) 若从高校B、C抽取的人中选2人作专题发言,求这二人都来自高校C的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com