练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
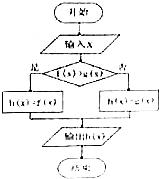
    7．如图所示的算法流程图中，若f（x）=lnx，g（x）=log2x，则h（4）的值等于（　　）
    A．1B．-1C．2D．ln4

    分析 分析程序中各变量、各语句的作用，再根据流程图所示的顺序，可知：该程序的作用是比较f（x）=lnx与g（x）=log2x的函数值，并输出其中的最大值．

    解答 解：分析程序中各变量、各语句的作用，
    再根据流程图所示的顺序，可知：
    该程序的作用是比较f（x）=lnx，g（x）=log2x，的函数值，
    并输出其中的最大值．
    当x=4时，f（4）=ln4，g（4）=log24=2，
    ∵2＞ln4，
    ∴h（4）=2．
    故选：C．

    点评 利用程序计算分段函数的值，一般要如下步骤①分析流程图的结构，分析是条件结构是如何嵌套的，以确定函数所分的段数；②根据判断框中的条件，设置分类标准；③根据判断框的“是”与“否”分支对应的操作，分析函数各段的解析式；④对前面的分类进行总结，写出分段函数的解析式；⑤将已知中的数据代入分段函数进行计算．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：解答题

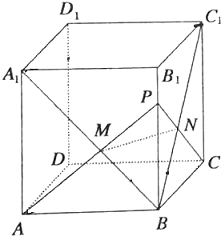    17．如图，在长方体ABCD-A1B1C1D1中，点P∈BB1（P不与B，B1重合）．PA∩A1B=M，PC∩BC1=N．
    求证：MN∥平面ABCD．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    18．已知函数g（x）=$\frac{1}{3}$x3+2x-m+$\frac{m}{x}$（m＞0）是[1，+∞）上的增函数．当实数m取最大值时，若存在点Q，使得过点Q的直线与曲线y=g（x）围成两个封闭图形，且这两个封闭图形的面积总相等，则点Q的坐标为（　　）
    A．（0，-3）B．（2，-3）C．（0，0）D．（0，3）

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    15．已知直线m⊥平面α，直线n在平面β内，给出下列三个命题：①“α∥β”是“m⊥n”的充分不必要条件；②“α⊥β”是“m∥n”的必要不充分条件；③“α⊥β”是“m⊥n”的充要条件．则其中真命题的个数为（　　）
    A．0B．1C．2D．3

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    2．已知a、b、c、R为常数，当x2+y2+z2=R2时，求函数f（x，y，z）=ax+by+cz的最大值与最小值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    12．已知数列{an}满足3an+1+an=4（n≥1），且a1=9．
    （1）求数列{an}的通项公式；
    （2）求数列{an}的前n项和Sn，并求满足不等式|Sn-n-6|$＜\frac{1}{125}$的最小正整数n．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    19．当k$∈（-\frac{1}{2}，0）$时，方程$\sqrt{|1-x|}$=-kx的解的个数是3．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

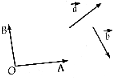    16．如图，已知向量$\overrightarrow{a}$，$\overrightarrow{b}$和$\overrightarrow{OA}$，$\overrightarrow{OB}$．求作：
    （1）向量$\overrightarrow{a}$分别在$\overrightarrow{OA}$，$\overrightarrow{OB}$方向上的分向量；
    （2）向量$\overrightarrow{b}$分别在$\overrightarrow{OA}$，$\overrightarrow{OB}$方向上的分向量．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    17．在矩形ABCD中，AB=6，AD=4，点P在边AB上，点Q在AD上，△CPQ的面积为8，则∠PCQ的最大值是30°．

    查看答案和解析>>

    同步练习册答案