
分析 (1)利用辅助角公式化积,再由正弦函数的值域得答案;
(2)令sinx+cosx=t,($-\sqrt{2}≤t≤\sqrt{2}$),求得sin2x=t2-1,转化为关于t的二次函数得答案.
解答 解:(1)∵y=sinx+cosx=$\sqrt{2}(\frac{\sqrt{2}}{2}•sinx+\frac{\sqrt{2}}{2}cosx)$=$\sqrt{2}sin(x+\frac{π}{4})$.
∴y∈[$-\sqrt{2},\sqrt{2}$];
(2)令sinx+cosx=t($-\sqrt{2}≤t≤\sqrt{2}$),
∴sin2x+2sinxcosx+cos2x=t2,则sin2x=t2-1,
∴y=sinx+cosx-sin2x=t-t2+1=-t2+t+1,($-\sqrt{2}≤t≤\sqrt{2}$),
对称轴方程为t=$\frac{1}{2}$,
∴当t=$\frac{1}{2}$时,${y}_{max}=\frac{5}{4}$;
当t=-$\sqrt{2}$时,${y}_{min}=-1-\sqrt{2}$.
∴y∈[$-1-\sqrt{2},\frac{5}{4}$].
点评 本题考查三角函数的化简求值,考查了三角函数值域的求法,训练了换元法求函数的值域,是中档题.


 浙江之星课时优化作业系列答案
浙江之星课时优化作业系列答案 激活思维优加课堂系列答案
激活思维优加课堂系列答案科目:高中数学 来源: 题型:选择题
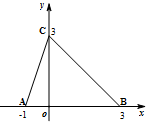
| A. | {x|-1≤x≤2} | B. | {x|-1<x≤2} | C. | {x|-1<x≤0} | D. | {x|-1<x≤3} |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 因为f(0)?f(2)>0,所以f(x)在(0,2)内没有零点 | |
| B. | 因为1是f(x)的一个零点,所以f(0)?f(2)<0 | |
| C. | 由于f(x)在区间(-∞,0)上单调递减,所以f(x)在(-∞,0)内有唯一的一个零点 | |
| D. | 以上说法都不对 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -$\frac{33}{65}$ | B. | $\frac{33}{65}$ | C. | $\frac{63}{65}$ | D. | $\frac{63}{65}$或$\frac{33}{65}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{5}{13}$ | B. | $-\frac{12}{13}$ | C. | $\frac{12}{13}$ | D. | $-\frac{5}{13}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
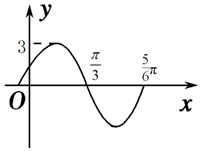 函数y=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示,则( )
函数y=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示,则( )| A. | f(x)的一个对称中心为$(\frac{4π}{3},0)$ | B. | f(x)的图象关于直线$x=-\frac{1}{12}π$ 对称 | ||
| C. | f(x)在$[-π,-\frac{π}{2}]$上是增函数 | D. | f(x)的周期为$\frac{π}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{2\sqrt{3}}{3}$ | B. | 2 | C. | $\sqrt{3}$ | D. | $\sqrt{5}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com