
【题目】已知方程(m2﹣2m﹣3)x+(2m2+m﹣1)y+5﹣2m=0(m∈R).
(1)求方程表示一条直线的条件;
(2)当m为何值时,方程表示的直线与x轴垂直;
(3)若方程表示的直线在两坐标轴上的截距相等,求实数m的值.
【答案】
(1)解:由 ![]() ,得:m=﹣1
,得:m=﹣1
∵方程(m2﹣2m﹣3)x+(2m2+m﹣1)y+5﹣2m=0(m∈R)表示直线
∴m2﹣2m﹣3、2m2+m﹣1不同时为0,∴m≠﹣1
(2)解:方程表示的直线与x轴垂直,∴ ![]() ,∴
,∴ ![]()
(3)解:当5﹣2m=0,即 ![]() 时,直线过原点,在两坐标轴上的截距均为0
时,直线过原点,在两坐标轴上的截距均为0
当 ![]() 时,由
时,由 ![]() 得:m=﹣2
得:m=﹣2
【解析】(1)由 ![]() ,得:m=﹣1,方程(m2﹣2m﹣3)x+(2m2+m﹣1)y+5﹣2m=0(m∈R)表示直线,可得m2﹣2m﹣3、2m2+m﹣1不同时为0,即可得出.(2)方程表示的直线与x轴垂直,可得
,得:m=﹣1,方程(m2﹣2m﹣3)x+(2m2+m﹣1)y+5﹣2m=0(m∈R)表示直线,可得m2﹣2m﹣3、2m2+m﹣1不同时为0,即可得出.(2)方程表示的直线与x轴垂直,可得 ![]() ,(3)当5﹣2m=0,即
,(3)当5﹣2m=0,即 ![]() 时,直线过原点,在两坐标轴上的截距均为0.当
时,直线过原点,在两坐标轴上的截距均为0.当 ![]() 时,由
时,由 ![]() ,解得:m.
,解得:m.
【考点精析】根据题目的已知条件,利用一般式方程的相关知识可以得到问题的答案,需要掌握直线的一般式方程:关于![]() 的二元一次方程
的二元一次方程![]() (A,B不同时为0).
(A,B不同时为0).


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】小王为了锻炼身体,每天坚持“健步走”,并用计步器进行统计.小王最近8天“健步走”步数的频数分布直方图(图1)及相应的消耗能量数据表(表1)如下:
健步走步数(前步) | 16 | 17 | 18 | 19 |
消耗能量(卡路里) | 400 | 440 | 480 | 520 |
(Ⅰ)求小王这8天“健步走”步数的平均数;
(Ⅱ)从步数为17千步,18千步,19千步的几天中任选2天,求小王这2天通过“健步走”消耗的能量和不小于1000卡路里的概率.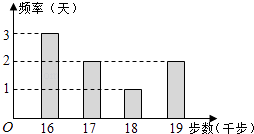
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,已知圆M的圆心在直线y=﹣2x上,且圆M与直线x+y﹣1=0相切于点P(2,﹣1).
(1)求圆M的方程;
(2)过坐标原点O的直线l被圆M截得的弦长为 ![]() ,求直线l的方程.
,求直线l的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了考查培育的某种植物的生长情况,从试验田中随机抽取100柱该植物进行检测,得到该植物高度的频数分布表如下:
组序 | 高度区间 | 频数 | 频率 |
1 | [230,235) | 14 | 0.14 |
2 | [235,240) | ① | 0.26 |
3 | [240,245) | ② | 0.20 |
4 | [245,250) | 30 | ③ |
5 | [250,255) | 10 | ④ |
合计 | 100 | 1.00 | |
(Ⅰ)写出表中①②③④处的数据;
(Ⅱ)用分层抽样法从第3、4、5组中抽取一个容量为6的样本,则各组应分别抽取多少个个体?
(Ⅲ)在(Ⅱ)的前提下,从抽出的容量为6的样本中随机选取两个个体进行进一步分析,求这两个个体中至少有一个来自第3组的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设数列{an}的前n项和为Sn , 已知S2=4,an+1=2Sn+1,n∈N* .
(1)求通项公式an;
(2)求数列{|an﹣n﹣2|}的前n项和.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设△ABC的三内角A、B、C成等差数列,sinA、sinB、sinC成等比数列,则这个三角形的形状是( )
A.直角三角形
B.钝角三角形
C.等腰直角三角形
D.等边三角形
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}满足a1=﹣2,an+1=2an+4.
(1)证明数列{an+4}是等比数列并求出{an}通项公式;
(2)若 ![]() ,求数列{bn}的前n项和Sn .
,求数列{bn}的前n项和Sn .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图1所示,在边长为24的正方形![]() 中,点
中,点![]() 在边
在边![]() 上,且
上,且![]() ,
, ![]() ,作
,作![]() 分别交
分别交![]() 、
、![]() 于点
于点![]() ,作
,作![]() 分别交
分别交![]() 于点
于点![]() ,将该正方形沿
,将该正方形沿![]() 折叠,使得
折叠,使得![]() 与
与![]() 重合,构成如图2所示的三棱柱
重合,构成如图2所示的三棱柱![]() .
.

(1)求证: ![]() 平面
平面![]() ;
;
(2)求多面体![]() 的体积.
的体积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com