
【题目】如图,建立平面直角坐标系xOy,x轴在地平面上,y轴垂直于地平面,单位长度为1千米.某炮位于坐标原点.已知炮弹发射后的轨迹在方程y=kx-![]() (1+k2)x2(k>0)表示的曲线上,其中k与发射方向有关.炮的射程是指炮弹落地点的横坐标.
(1+k2)x2(k>0)表示的曲线上,其中k与发射方向有关.炮的射程是指炮弹落地点的横坐标.
设在第一象限有一飞行物(忽略其大小),其飞行高度为3.2千米,试问它的横坐标a不超过多少时,炮弹可以击中它?请说明理由.

 发散思维新课堂系列答案
发散思维新课堂系列答案科目:高中数学 来源: 题型:
【题目】如图,四边形ABCD为菱形,G为AC与BD的交点,BE⊥平面ABCD,
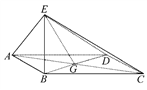
(1)证明:平面AEC⊥平面BED.
(2)若∠ABC=120°,AE⊥EC,三棱锥E-ACD的体积为![]() ,求该三棱锥的侧面积.
,求该三棱锥的侧面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】线段AB的两端在直二面角α-l-β的两个面内,并与这两个面都成30°角,则异面直线AB与l所成的角是( )
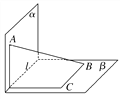
A. 30° B. 45°
C. 60° D. 75°
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】近年来,我国电子商务蓬勃发展. 2016年“618”期间,某网购平台的销售业绩高达516亿元人民币,与此同时,相关管理部门推出了针对该网购平台的商品和服务的评价系统. 从该评价系统中选出200次成功交易,并对其评价进行统计,网购者对商品的满意率为0.6,对服务的满意率为0.75,其中对商品和服务都满意的交易为80次.
(Ⅰ) 根据已知条件完成下面的![]() 列联表,并回答能否有99%的把握认为“网购者对商品满意与对服务满意之间有关系”?
列联表,并回答能否有99%的把握认为“网购者对商品满意与对服务满意之间有关系”?
对服务满意 | 对服务不满意 | 合计 | |
对商品满意 | 80 | ||
对商品不满意 | |||
合计 | 200 |
(Ⅱ) 若将频率视为概率,某人在该网购平台上进行的3次购物中,设对商品和服务都满意的次数为随机变量![]() ,求
,求![]() 的分布列和数学期望
的分布列和数学期望![]() .
.
附:![]()
![]() (其中
(其中![]() 为样本容量)
为样本容量)
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() .
.
(Ⅰ)若f(1)=0,求函数f(x)的最大值;
(Ⅱ)令![]() ,讨论函数g(x)的单调区间;
,讨论函数g(x)的单调区间;
(Ⅲ)若a=2,正实数x1,x2满足![]() 证明
证明![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】国际奥委会将于2017年9月15日在秘鲁利马召开130次会议决定2024年第33届奥运
会举办地。目前德国汉堡、美国波士顿等申办城市因市民担心赛事费用超支而相继退出。某机构为调查我国公民对申办奥运会的态度,选了某小区的100位居民调查结果统计如下:
支持 | 不支持 | 合计 | |
年龄不大于50岁 | 80 | ||
年龄大于50岁 | 10 | ||
合计 | 70 | 100 |
(1)根据已有数据,把表格数据填写完整;
(2)能否在犯错误的概率不超过5%的前提下认为不同年龄与支持申办奥运无关?
(3)已知在被调查的年龄大于50岁的支持者中有5名女性,其中2位是女教师,现从这5名女性中随机抽取3人,求至多有1位教师的概率.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C: ![]() (a>b>0)的离心率为
(a>b>0)的离心率为![]() ,以原点O为圆心,椭圆的短半轴长为半径的圆与直线x﹣y+
,以原点O为圆心,椭圆的短半轴长为半径的圆与直线x﹣y+![]() =0相切.
=0相切.
(Ⅰ)求椭圆C的标准方程;
(Ⅱ)若直线l:y=kx+m与椭圆C相交于A、B两点,且kOAkOB=﹣![]() ,判断△AOB的面积是否为定值?若为定值,求出定值;若不为定值,说明理由.
,判断△AOB的面积是否为定值?若为定值,求出定值;若不为定值,说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com