
【题目】如图,在四棱锥![]() 中,
中,![]() 底面
底面![]() ,
,![]() 为直角,
为直角,![]() ,
,![]() ,
,![]() 、
、![]() 分别为
分别为![]() 、
、![]() 的中点.
的中点.
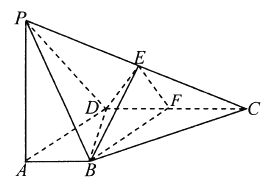
(I)证明:平面![]() 平面
平面![]() ;
;
(II)设![]() ,且二面角
,且二面角![]() 的平面角大于
的平面角大于![]() ,求
,求![]() 的取值范围.
的取值范围.
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=ex![]() (x﹣a)2+4.
(x﹣a)2+4.
(1)若f(x)在(﹣∞,+∞)上单调递增,求a的取值范围;
(2)若x≥0,不等式f(x)≥0恒成立,求a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某市准备引进优秀企业进行城市建设. 城市的甲地、乙地分别对5个企业(共10个企业)进行综合评估,得分情况如茎叶图所示.

(Ⅰ)根据茎叶图,求乙地对企业评估得分的平均值和方差;
(Ⅱ)规定得分在85分以上为优秀企业. 若从甲、乙两地准备引进的优秀企业中各随机选取1个,求这两个企业得分的差的绝对值不超过5分的概率.
注:方差![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设命题p:实数x满足x2-2ax-3a2<0(a>0),命题q:实数x满足![]() ≥0.
≥0.
(Ⅰ)若a=1,p,q都为真命题,求x的取值范围;
(Ⅱ)若q是p的充分不必要条件,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】齐王有上等,中等,下等马各一匹;田忌也有上等,中等,下等马各一匹.田忌的上等马优于齐王的中等马,劣于齐王的上等马;田忌的中等马优于齐王的下等马,劣于齐王的中等马;田忌的下等马劣于齐王的下等马.现从双方的马匹中随机各选一匹进行一场比赛,若有优势的马一定获胜,则齐王的马获胜的概率为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com