
【题目】关于函数f(x)=5sin3x+5 ![]() cos3x,下列说法正确的是( )
cos3x,下列说法正确的是( )
A.函数f(x)关于x= ![]() π对称
π对称
B.函数f(x)向左平移 ![]() 个单位后是奇函数
个单位后是奇函数
C.函数f(x)关于点( ![]() ,0)中心对称
,0)中心对称
D.函数f(x)在区间[0, ![]() ]上单调递增
]上单调递增
【答案】D
【解析】解:对于函数f(x)=5sin3x+5 ![]() cos3x=10(
cos3x=10( ![]() sin3x+
sin3x+ ![]() cos3x)=10sin(3x+
cos3x)=10sin(3x+ ![]() ), 令3x+
), 令3x+ ![]() =kπ+
=kπ+ ![]() ,求得x=
,求得x= ![]() +
+ ![]() ,k∈Z,可得函数的图象关于直线x=
,k∈Z,可得函数的图象关于直线x= ![]() +
+ ![]() ,k∈Z对称,故A错误.
,k∈Z对称,故A错误.
把函数f(x)向左平移 ![]() 个单位后得到y=10sin[3(x+
个单位后得到y=10sin[3(x+ ![]() )+
)+ ![]() ]=10sin(3x+
]=10sin(3x+ ![]() )=10cos3x的图象,为偶函数,故B错误.
)=10cos3x的图象,为偶函数,故B错误.
令x= ![]() ,求得f(x)=10,为函数的最大值,故函数的图象关于直线x=
,求得f(x)=10,为函数的最大值,故函数的图象关于直线x= ![]() 对称,故C错误.
对称,故C错误.
在区间[0, ![]() ]上,3x+
]上,3x+ ![]() ∈[
∈[ ![]() ,
, ![]() ],故函数f(x)在区间[0,
],故函数f(x)在区间[0, ![]() ]上单调递增,故D正确.
]上单调递增,故D正确.
故选:D.
【考点精析】认真审题,首先需要了解函数y=Asin(ωx+φ)的图象变换(图象上所有点向左(右)平移![]() 个单位长度,得到函数
个单位长度,得到函数![]() 的图象;再将函数
的图象;再将函数![]() 的图象上所有点的横坐标伸长(缩短)到原来的
的图象上所有点的横坐标伸长(缩短)到原来的![]() 倍(纵坐标不变),得到函数
倍(纵坐标不变),得到函数![]() 的图象;再将函数
的图象;再将函数![]() 的图象上所有点的纵坐标伸长(缩短)到原来的
的图象上所有点的纵坐标伸长(缩短)到原来的![]() 倍(横坐标不变),得到函数
倍(横坐标不变),得到函数![]() 的图象).
的图象).


 作业辅导系列答案
作业辅导系列答案科目:高中数学 来源: 题型:
【题目】如图,已知椭圆C: ![]() =1(a>b>0)的离心率为
=1(a>b>0)的离心率为 ![]() ,以椭圆C的左顶点T为圆心作圆T:(x+2)2+y2=r2(r>0),设圆T与椭圆C交于点M与点N.
,以椭圆C的左顶点T为圆心作圆T:(x+2)2+y2=r2(r>0),设圆T与椭圆C交于点M与点N. 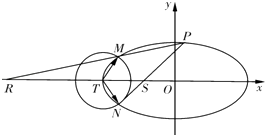
(1)求椭圆C的方程;
(2)求 ![]() 的最小值,并求此时圆T的方程;
的最小值,并求此时圆T的方程;
(3)设点P是椭圆C上异于M,N的任意一点,且直线MP,NP分别与x轴交于点R,S,O为坐标原点,求证:|OR||OS|为定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】我们把离心率e= ![]() 的双曲线
的双曲线 ![]() =1(a>0,b>0)称为黄金双曲线.如图是双曲线
=1(a>0,b>0)称为黄金双曲线.如图是双曲线 ![]() =1(a>0,b>0,c=
=1(a>0,b>0,c= ![]() )的图象,给出以下几个说法: ①若b2=ac,则该双曲线是黄金双曲线;
)的图象,给出以下几个说法: ①若b2=ac,则该双曲线是黄金双曲线;
②若F1 , F2为左右焦点,A1 , A2为左右顶点,B1(0,b),B2(0,﹣b)且∠F1B1A2=90°,则该双曲线是黄金双曲线;
③若MN经过右焦点F2且MN⊥F1F2 , ∠MON=90°,则该双曲线是黄金双曲线.
其中正确命题的序号为 . 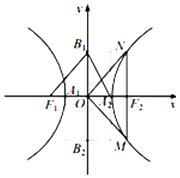
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】定义在R上的函数f(x)= ![]() x3+cx+3(c为常数),f(x)在x=0处的切线与直线y=x+2垂直.
x3+cx+3(c为常数),f(x)在x=0处的切线与直线y=x+2垂直.
(1)求函数y=f(x)的解析式;
(2)设g(x)=4lnx﹣f′(x),(其中f′(x)是函数f(x)的导函数),求g(x)的极值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设锐角三角形ABC的内角A,B,C的对边分别为a,b,c,且a=2bsin A. (Ⅰ)求角B的大小;
(Ⅱ)若a= ![]() ,c=5,求△ABC的面积及b.
,c=5,求△ABC的面积及b.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在杨辉三角形中,斜线l的上方从1按箭头所示方向可以构成一个“锯齿形”的数列:1,3,3,4,6,5,10,…,记此数列的前n项之和为Sn , 则S21的值为( ) 
A.66
B.153
C.295
D.361
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知不等式|x+2|+|x﹣2|<18的解集为A.
(1)求A;
(2)若a,b∈A,x∈(0,+∞),不等式a+b<x ![]() +m恒成立,求实数m的取值范围.
+m恒成立,求实数m的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com