【题目】已知
．
（Ⅰ）当
在
处切线的斜率为
，求
的值；
（Ⅱ）在（Ⅰ）的前提下，求
的极值；
（Ⅲ）若
有
个不同零点，求
的取值范围．．
【答案】(1) 
(2) 
，无极大值（3） 
【解析】试题分析：（Ⅰ）求导，利用导数的几何意义进行求解；（Ⅱ）利用导函数的符号变换确定函数的单调性，进而确定函数的极值；（Ⅲ）求导，讨论
的范围，研究函数的单调性和极值，通过零点的个数确定极值的符号进行求解.
试题解析:（Ⅰ）
，
∴
（Ⅱ）当
时 
， 
， 
为减函数
， 
， 
为增函数
∴
，无极大值
（Ⅲ）
当
时， 
，只有个零点
当
时， 
， 
， 
为减函数
， 
， 
为增函数
而
∴当
， 
，使
当
时，∴
∴
∴
取
，∴
， 
∴函数有
个零点
当
时， 
令
得
， 
①
，即
时
当
变化时 
， 
变化情况是
|
|
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
∴
∴函数
至多有个零点，不符合题意
②
时， 
， 
在
单调递增
∴
至多有个零点，不合题意
③当
时，即
时
当
变化时
， 
的变化情况是
， 
时， 
即
，∴函数
至多有个零点，
综上： 
的取值范围是
.
科目：高中数学 来源： 题型：
【题目】已知曲线
， 
，则下列说法正确的是（ ）
A. 把
上各点横坐标伸长到原来的2倍，纵坐标不变，再把得到的曲线向右平移
个单位长度，得到曲线
B. 把
上各点横坐标伸长到原来的2倍，纵坐标不变，再把得到的曲线向右平移
个单位长度，得到曲线
C. 把曲线
向右平移
个单位长度，再把得到的曲线上各点横坐标缩短到原来的
，纵坐标不变，得到曲线
D. 把曲线
向右平移
个单位长度，再把得到的曲线上各点横坐标缩短到原来的
，纵坐标不变，得到曲线
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】如图,在四棱锥
中,底面
为正方形,平面
底面
, 
,点
分别是
的中点.
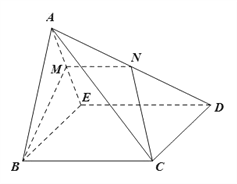
（Ⅰ）求证: 
平面
;
（Ⅱ）求证: 
平面
;
（Ⅲ）在棱
上求作一点
,使得
,并说明理由.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知椭圆
：
的左、右有顶点分别是
、
，上顶点是
，圆
：
的圆心到直线
的距离是
，且椭圆的右焦点与抛物线
的焦点重合．
（Ⅰ）求椭圆的方程；
（Ⅱ）平行于
轴的动直线与椭圆和圆在第一象限内的交点分别为
、
，直线
、
与
轴的交点记为
，
．试判断
是否为定值，若是，证明你的结论．若不是，举反例说明．
查看答案和解析>>
科目：高中数学 来源： 题型：
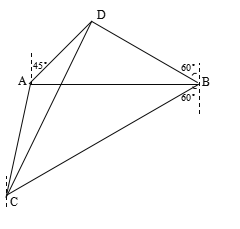
【题目】如图，A、B是海面上位于东西方向相距
海里的两个观测点.现位于A点北偏东45°，B点北偏西60°的D点有一艘轮船发出求救信号.位于B点南偏西60°且与B相距20
海里的C点的救援船立即前往营救，其航行速度为30海里/小时。求救援船直线到达D的时间和航行方向.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】为调查某社区年轻人的周末生活状况，研究这一社区年轻人在周末的休闲方式与性别的关系，随机调查了该社区年轻人80人，得到下面的数据表：
（1）将此样本的频率估计为总体的概率，随机调查3名在该社区的年轻男性，设调查的3人在这一时间段以上网为休闲方式的人数为随机变量X,求X的分布列和数学期望；
（2）根据以上数据，能否有99%的把握认为“周末年轻人的休闲方式与性别有关系”？
参考公式：
参考数据：
| 0.05 | 0.010 |
| 3.841 | 6.635 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
