
分析 (1)求出函数的导数,解关于导函数的不等式,求出函数的单调区间,从而求出函数的最小值即可;
(2)求出函数的导数,解关于导函数的不等式,求出函数的最小值,结合题意从而求出a的范围即可.
解答 解:(1)由已知得$0<x<1,G'(x)=lnx-ln({1-x})=ln\frac{x}{1-x}$…(1分)
令G'(x)<0,得$0<x<\frac{1}{2}$;令G'(x)>0,得$\frac{1}{2}<x<1$,
所以G(x)的单调减区间为$({0,\frac{1}{2}})$,单调增区间为$({\frac{1}{2},1})$…(3分)
从而$G{(x)_{min}}=G({\frac{1}{2}})=ln\frac{1}{2}=-ln2$…(4分)
(2)由(1)中c=-ln2得$f(x)=a•{e^x}+\frac{a+1}{x}-2({a+1})$…(5分)
所以$f'(x)=\frac{{a{x^2}•{e^x}-({a+1})}}{x^2}$…(6分)
令g(x)=ax2•ex-(a+1),则g'(x)=ax(2+x)ex>0…(7分)
所以g(x)在(0,+∞)上单调递增,
因为g(0)=-(a+1),且当x→+∞时,g(x)>0,
所以存在x0∈(0,+∞),使g(x0)=0,
且f(x)在(0,x0)上单调递减,在(x0,+∞)上单调递增…(8分)
因为$g({x_0})=ax_0^2•{e^{x_0}}-({a+1})=0$,所以$ax_0^2•{e^{x_0}}=a+1$,
即$a•{e^{x_0}}=\frac{a+1}{x_0^2}$,因为对于任意的x∈(0,+∞),恒有f(x)≥0成立,
所以$f{(x)_{min}}=f({x_0})=a•{e^{x_0}}+\frac{a+1}{x_0}-2({a+1})≥0$…(9分)
所以$\frac{a+1}{x_0^2}+\frac{a+1}{x_0}-2({a+1})≥0$,即$\frac{1}{x_0^2}+\frac{1}{x_0}-2≥0$,
亦即$2x_0^2-{x_0}-1≤0$,所以$-\frac{1}{2}≤{x_0}≤1$…(10分)
因为$ax_0^2•{e^{x_0}}=a+1$,所以$x_0^2•{e^{x_0}}=\frac{a+1}{a}>1$,
又x0>0,所以0<x0≤1,从而$x_0^2•{e^{x_0}}≤e$,
所以$1<\frac{a+1}{a}≤e$,故$a≥\frac{1}{e-1}$…(12分)
点评 本题考查了函数的单调性、最值问题,考查导数的应用以及函数恒成立问题,是一道综合题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
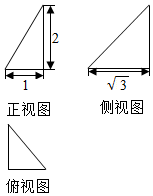 某几何体的三视图如图所示,则该几何体外接球的表面积为( )
某几何体的三视图如图所示,则该几何体外接球的表面积为( )| A. | $\frac{25π}{4}$ | B. | $\frac{25π}{8}$ | C. | 12π | D. | 8π |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
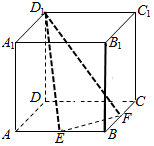 如图,正方体ABCD-A1B1C1D1中,E、F分别是AB、BC的中点,过点D1、E、F的截面将正方体分割成两个部分,记这两个部分的体积分别为V1、V2(V1<V2),则V1:V2=( )
如图,正方体ABCD-A1B1C1D1中,E、F分别是AB、BC的中点,过点D1、E、F的截面将正方体分割成两个部分,记这两个部分的体积分别为V1、V2(V1<V2),则V1:V2=( )| A. | $\frac{1}{3}$ | B. | $\frac{3}{5}$ | C. | $\frac{25}{47}$ | D. | $\frac{7}{9}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | $\frac{{\sqrt{3}}}{2}$ | C. | $\sqrt{5}$ | D. | $\frac{{\sqrt{5}}}{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com