
【题目】某工厂共有![]() 名工人,已知这
名工人,已知这![]() 名工人去年完成的产品数都在区间
名工人去年完成的产品数都在区间![]() (单位:万件)内,其中每年完成
(单位:万件)内,其中每年完成![]() 万件及以上的工人为优秀员工,现将其分成
万件及以上的工人为优秀员工,现将其分成![]() 组,第
组,第![]() 组、第
组、第![]() 组、第
组、第![]() 组、第
组、第![]() 组、第
组、第![]() 组对应的区间分别为
组对应的区间分别为![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,并绘制出如图所示的频率分布直方图.
,并绘制出如图所示的频率分布直方图.
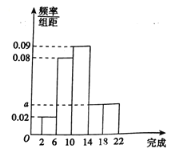
(1)求![]() 的值,并求去年优秀员工人数;
的值,并求去年优秀员工人数;
(2)选取合适的抽样方法从这![]() 名工人中抽取容量为
名工人中抽取容量为![]() 的样本,求这
的样本,求这![]() 组分别应抽取的人数;
组分别应抽取的人数;
(3)现从(2)中![]() 人的样本中的优秀员工中随机选取
人的样本中的优秀员工中随机选取![]() 名传授经验,求选取的
名传授经验,求选取的![]() 名工人在同一组的概率.
名工人在同一组的概率.
【答案】(1)![]() ,去年优秀员工人数为
,去年优秀员工人数为![]() ;(2)用分层抽样,这
;(2)用分层抽样,这![]() 组分别应抽取的人数依次为
组分别应抽取的人数依次为![]() ;(3)
;(3)![]() .
.
【解析】
(1)由频率分布直方图中所有小长方形的面积和为1可求得![]() 的值,进而可得优秀员工人数.
的值,进而可得优秀员工人数.
(2)分层抽样,按比例确定各组应抽取的人数.
(3)列出所有的基本事件数和所求事件包含的基本事件数,由古典概型得出概率.
(1)∵![]() ,∴
,∴![]() .
.
去年优秀员工的人数为![]() .
.
(2)用分层抽样比较合适.
第![]() 组应抽取的人数为
组应抽取的人数为![]() ,
,
第![]() 组应抽取的人数为
组应抽取的人数为![]() ,
,
第![]() 组应抽取的人数为
组应抽取的人数为![]() ,
,
第![]() 组应抽取的人数为
组应抽取的人数为![]() ,
,
第![]() 组应抽取的人数为
组应抽取的人数为![]() .
.
(3)从(2)中![]() 人的样本中的优秀员工中,
人的样本中的优秀员工中,
第![]() 组有
组有![]() 人,记这
人,记这![]() 人分别为
人分别为![]() ,
,![]() ,
,![]() ;
;
第![]() 组有
组有![]() 人,记这
人,记这![]() 人分别为
人分别为![]() ,
,![]() ,
,![]() .
.
从这![]() 人中随机选取
人中随机选取![]() 名,所有的基本事件为
名,所有的基本事件为
![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,
共有![]() 个基本事件.
个基本事件.
选取的![]() 名工人在同一组的基本事件有
名工人在同一组的基本事件有![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 共
共![]() 个,
个,
故所求概率为![]() .
.


科目:高中数学 来源: 题型:
【题目】如图,在多面体![]() 中,四边形
中,四边形![]() 为矩形,
为矩形,![]() ,
,![]() 均为等边三角形,
均为等边三角形,![]() ,
,![]() .
.

(1)过![]() 作截面与线段
作截面与线段![]() 交于点
交于点![]() ,使得
,使得![]() 平面
平面![]() ,试确定点
,试确定点![]() 的位置,并予以证明;
的位置,并予以证明;
(2)在(1)的条件下,求直线![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了在夏季降温和冬季取暖时减少能源消耗,业主决定对房屋的屋顶和外墙喷涂某种新型隔热材料,该材料有效使用年限为20年.已知房屋外表喷一层这种隔热材料的费用为每毫米厚6万元,且每年的能源消耗费用![]() (万元)与隔热层厚度
(万元)与隔热层厚度![]() (毫米)满足关系:
(毫米)满足关系:![]() .设
.设![]() 为隔热层建造费用与
为隔热层建造费用与![]() 年的能源消耗费用之和.
年的能源消耗费用之和.
(1)请解释![]() 的实际意义,并求
的实际意义,并求![]() 的表达式;
的表达式;
(2)当隔热层喷涂厚度为多少毫米时,业主所付的总费用![]() 最少?并求此时与不建隔热层相比较,业主可节省多少钱?
最少?并求此时与不建隔热层相比较,业主可节省多少钱?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某次招聘分为笔试和面试两个环节,且只有笔试过关者方可进入面试环节,笔试与面试都过关才会被录用.笔试需考完全部三科,且至少有两科优秀才算笔试过关,面试需考完全部两科且两科均为优秀才算面试过关.假设某考生笔试三科每科优秀的概率均为![]() ,面试两科每科优秀的概率均为
,面试两科每科优秀的概率均为![]() .
.
(1)求该考生被录用的概率;
(2)设该考生在此次招聘活动中考试的科目总数为![]() ,求
,求![]() 的分布列与数学期望.
的分布列与数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,用![]() 种不同的颜色给图中的
种不同的颜色给图中的![]() 个格子涂色,每个格子涂一种颜色,要求最多使用
个格子涂色,每个格子涂一种颜色,要求最多使用![]() 种颜色且相邻的两个格子颜色不同,则不同的涂色方法共有( )
种颜色且相邻的两个格子颜色不同,则不同的涂色方法共有( )
A.![]() 种B.
种B.![]() 种C.
种C.![]() 种D.
种D.![]() 种
种
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】随着手机的发展,“微信”逐渐成为人们交流的一种形式,某机构对“使用微信交流”的态度进行调查,随机抽取了50人,他们年龄的频数分布及对“使用微信交流”赞成人数如表:
年龄(单位:岁) |
|
|
|
|
|
|
频数 | 5 | 10 | 15 | 10 | 5 | 5 |
赞成人数 | 5 | 10 | 12 | 7 | 2 | 1 |
(1)若以“年龄55岁为分界点”,由以上统计数据完成下面![]() 列联表,并判断是否有99.9%的把握认为“使用微信交流”的态度与人的年龄有关;
列联表,并判断是否有99.9%的把握认为“使用微信交流”的态度与人的年龄有关;
年龄不低于55岁的人数于 | 年龄低于55岁的人数 | 合计 | |
赞成 | |||
不赞成 | |||
合计 |
(2)若从年龄在![]() 的被调查人中随机选取2人进行追踪调查,求2人中至少有1人赞成“使用微信交流”的概率.
的被调查人中随机选取2人进行追踪调查,求2人中至少有1人赞成“使用微信交流”的概率.
参考数据:
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
![]() ,其中
,其中![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com