
����Ŀ��ѧУ�ӲμӸ߶��꼶��ĩ���Ե�ѧ���г��һЩѧ������ͳ�������ǵ���ѧ�ɼ����ɼ���Ϊ����������Ϊ100�֣������������������г�������Ƶ�ʷֲ�����
���� | Ƶ�� | Ƶ�� |
[40��50�� | A | 0.04 |
[50��60�� | 4 | 0.08 |
[60��70�� | 20 | 0.40 |
[70��80�� | 15 | 0.30 |
[80��90�� | 7 | B |
[90��100] | 2 | 0.04 |
�ϼ� | C | 1 |
��1���ڸ���������Ƶ�ʷֲ����У���A��B��C��ֵ��
��2����ȫƵ�ʷֲ�ֱ��ͼ��������������ȫ��߶��꼶ѧ����ĩ��ѧ�ɼ�����������λ����
��3���ִӷ�����[80��90����[90��100]��9��ͬѧ�������ȡ����ͬѧ����ȡ������ѧ��������������90�ֵĸ��ʣ�
���𰸡���1��2��0.14��50��2��65�� 69.5��3��![]() ��
��
��������
(1)����Ƶ�ʷֲ���,���Ƶ��,ֱ�����![]() ,
,![]() ,
,![]() ��ֵ;
��ֵ;
(2)�������,��λ��,����Ƶ�ʷֲ�ֱ��ͼ����;
(3)���ùŵ�����ʵ���,�����ʼ���.
(1)![]() ;
;
(2)����Ϊ��ߵ�С���������е�65,
��λ��Ϊ![]() ,
,
Ƶ��ֱ��ͼ����:
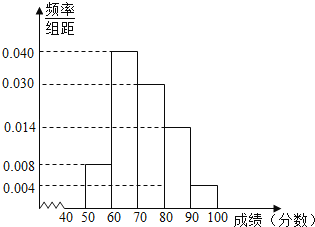
(3)����={�ӷ�����[80,100]��10��ͬѧ�������ȡ����ͬѧ},
![]() ,
,
A={����ѧ��������������90��},n(A)=1,
���ݹŵ���ͼ��㹫ʽ�ɵ�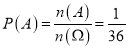 .
.


 ��ʦ������Ԫ��ĩ���100��ϵ�д�
��ʦ������Ԫ��ĩ���100��ϵ�д� ��У������Ԫͬ��ѵ��������ϵ�д�
��У������Ԫͬ��ѵ��������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������![]() Ϊ������������У���
Ϊ������������У���![]() Ϊ�����Σ�
������![]() ��
��![]() ���Ҷ����
���Ҷ����![]() ������
������![]() ����
����![]() .
.
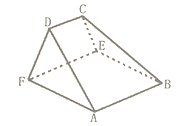
��1��֤����![]() ƽ��
ƽ��![]() ��
��
��2����ֱ��![]() ��ƽ��
��ƽ��![]() ���ɽǵ�����ֵ.
���ɽǵ�����ֵ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����f��x��=ex-m��x+1��+1��m��R����
��1��������f��x���ļ�СֵΪ1����ʵ��m��ֵ��
��2����x��0ʱ������ʽ![]() ���������ʵ��m��ȡֵ��Χ��
���������ʵ��m��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������P����F��0��1���ľ��������ֱ��y����2�ľ�����1����P�Ĺ켣C�ķ���Ϊ_____�������㣨2��1����������C������l��������l�ķ���Ϊ_____
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������P��ABCD�У��ı���ABCD�����Σ�![]() ��BD��2��
��BD��2��
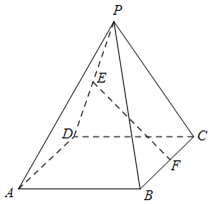
��1������E��F�ֱ�Ϊ�߶�PD��BC�ϵ��е㣬��֤��EF��ƽ��PAB��
��2����ƽ��PBD��ƽ��ABCD����PD��PB��PD��PB����ƽ��PAB��ƽ��PBC���ɵ������ǵ�����ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����x��һԪ���κ���f��x����ax2��2bx+8��
��1���輯��P��{1��2��3}��Q��{2��3��4��5}���ֱ�Ӽ���P��Q�����ȡһ������Ϊa��b������y��f��x�������䣨������2]���������Ϊ�������ĸ��ʣ�
��2���輯��P��[1��3]��Q[2��5]���ֱ�Ӽ���P��Q�����ȡһ��ʵ����Ϊa��b������y��f��x�������䣨������2]���������Ϊ�������ĸ��ʣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪������C��y2=4x�Ľ���ΪF������F��б��Ϊ1��ֱ����������C����A��B���㣬�������߶�ABΪֱ����Բ�ϴ�������M��N����ֱ��![]() ��x+y+a=0�ϴ���һ��Q��ʹ����MQN=90������ʵ��a��ȡֵ��ΧΪ��������
��x+y+a=0�ϴ���һ��Q��ʹ����MQN=90������ʵ��a��ȡֵ��ΧΪ��������
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������![]() �У�����
�У�����![]() Ϊ���Σ�ֱ��
Ϊ���Σ�ֱ��![]() ƽ��
ƽ��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() �ϵ�һ�㣬
�ϵ�һ�㣬![]() .
.
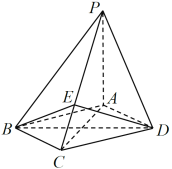
��1��֤����ֱ��![]() ƽ��
ƽ��![]() ��
��
��2����![]() ��������
��������![]() ������ֵ.
������ֵ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��ǡ�ABC�У���A��B��C�ĶԱ߷ֱ�Ϊa��b��c��b+c=10��a=![]() ��5bsinAcosC+5csinAcosB=3a��
��5bsinAcosC+5csinAcosB=3a��
��1����A������ֵ��
��2����b��c��
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com