
 定义在区间
定义在区间 上的函数y=f(x)的图象关于直线
上的函数y=f(x)的图象关于直线 对称,当
对称,当 时,函数f(x)=Asin(ωx+φ),
时,函数f(x)=Asin(ωx+φ), ,其图象如图.
,其图象如图. 上的表达式;
上的表达式; 的解集.
的解集.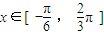 时,:
时,: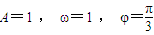 ,再由函数y=f(x)的图象关于直线
,再由函数y=f(x)的图象关于直线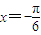 对称求出
对称求出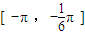 上的解析式,即可得到函数y=f(x)在
上的解析式,即可得到函数y=f(x)在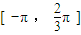 的表达式;
的表达式;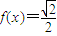 的解.
的解. 时,
时,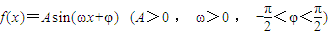 ,观察图象易得:A=1,周期为2π,可得ω=1,
,观察图象易得:A=1,周期为2π,可得ω=1,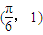 代入,结合题设可得φ=
代入,结合题设可得φ=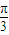 ,即函数
,即函数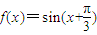 ,
,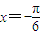 对称得,
对称得, 时,函数f(x)=-sinx.
时,函数f(x)=-sinx.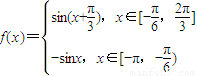 .
.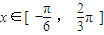 时,
时,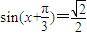 得,
得,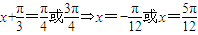 ;
;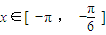 时,由
时,由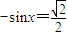 得,
得,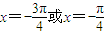 .
.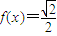 的解集为
的解集为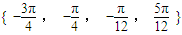


 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案科目:高中数学 来源: 题型:
已知定义在区间![]() 上的函数y=f(x)的图象关于直线
上的函数y=f(x)的图象关于直线![]() 对称,当
对称,当![]() 时,函数f(x)=sinx.
时,函数f(x)=sinx.
(1)求![]() ,
,![]() 的值;
的值;
(2)求y=f(x)的函数表达式;
(3)如果关于x的方程f(x)=a有解,那么将方程在a取某一确定值时所求得的所有解的和记为Ma,求Ma的所有可能取值及相对应的a的取值范围.
查看答案和解析>>
科目:高中数学 来源:2011年山东省烟台市招远一中高考数学模拟试卷(1)(解析版) 题型:解答题
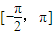 上的函数y=f(x)的图象关于直线
上的函数y=f(x)的图象关于直线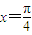 对称,当
对称,当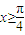 时,函数f(x)=sinx.
时,函数f(x)=sinx.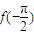 ,
,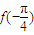 的值;
的值;查看答案和解析>>
科目:高中数学 来源:2010年高考试题分项版理科数学之专题六不等式 题型:填空题
定义在区间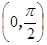 上的函数y=6cosx的图像与y=5tanx的图像的交点为P,过点P作PP1⊥x轴于点P1,直线PP1与y=sinx的图像交于点P2,则线段P1P2的长为_______ _____
上的函数y=6cosx的图像与y=5tanx的图像的交点为P,过点P作PP1⊥x轴于点P1,直线PP1与y=sinx的图像交于点P2,则线段P1P2的长为_______ _____
查看答案和解析>>
科目:高中数学 来源:2010年高考试题分项版理科数学之专题二函数 题型:填空题
定义在区间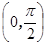 上的函数y=6cosx的图像与y=5tanx的图像的交点为P,过点P作PP1⊥x轴于点P1,直线PP1与y=sinx的图像交于点P2,则线段P1P2的长为_______ _____
上的函数y=6cosx的图像与y=5tanx的图像的交点为P,过点P作PP1⊥x轴于点P1,直线PP1与y=sinx的图像交于点P2,则线段P1P2的长为_______ _____
查看答案和解析>>
科目:高中数学 来源:2010年高考试题(江苏版)解析版 题型:填空题
定义在区间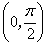 上的函数y=6cosx的图像与y=5tanx的图像的交点为P,过点P作PP1⊥x轴于点P1,直线PP1与y=sinx的图像交于点P2,则线段P1P2的长为_______▲_____。
上的函数y=6cosx的图像与y=5tanx的图像的交点为P,过点P作PP1⊥x轴于点P1,直线PP1与y=sinx的图像交于点P2,则线段P1P2的长为_______▲_____。
且其中的x满足6cosx=5tanx,解得sinx=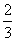 。线段P1P2的长为
。线段P1P2的长为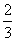
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com