
【题目】“工资条里显红利,个税新政人民心”.随着2019年新年钟声的敲响,我国自1980年以来,力度最大的一次个人所得税(简称个税)改革迎来了全面实施的阶段.2019年1月1日实施的个税新政主要内容包括:(1)个税起征点为5000元;(2)每月应纳税所得额(含税)=收入-个税起征点-专项附加扣除;(3)专项附加扣除包括住房、子女教育和赡养老人等.
新旧个税政策下每月应纳税所得额(含税)计算方法及其对应的税率表如下:
旧个税税率表(个税起征点3500元) | 新个税税率表(个税起征点5000元) | |||
缴税级数 | 每月应纳税所得额(含税)=收入-个税起征点 | 税率(%) | 每月应纳税所得额(含税)=收入-个税起征点-专项附加扣除 | 税率(%) |
1 | 不超过1500元部分 | 3 | 不超过3000元部分 | 3 |
2 | 超过1500元至4500元部分 | 10 | 超过3000元至12000元部分 | 10 |
3 | 超过4500元至9000元的部分 | 20 | 超过12000元至25000元的部分 | 20 |
4 | 超过9000元至35000元的部分 | 25 | 超过25000元至35000元的部分 | 25 |
5 | 超过35000元至55000元部分 | 30 | 超过35000元至55000元部分 | 30 |
··· | ··· | ··· | ··· | ··· |
随机抽取某市1000名同一收入层级的![]() 从业者的相关资料,经统计分析,预估他们2019年的人均月收入24000元.统计资料还表明,他们均符合住房专项扣除;同时,他们每人至多只有一个符合子女教育扣除的孩子,并且他们之中既不符合子女教育扣除又不符合赡养老人扣除、只符合子女教育扣除但不符合赡养老人扣除、只符合赡养老人扣除但不符合子女教育扣除、即符合子女教育扣除又符合赡养老人扣除的人数之比是2:1:1:1;此外,他们均不符合其他专项附加扣除.新个税政策下该市的专项附加扣除标准为:住房1000元/月,子女教育每孩1000元/月,赡养老人2000元/月等。
从业者的相关资料,经统计分析,预估他们2019年的人均月收入24000元.统计资料还表明,他们均符合住房专项扣除;同时,他们每人至多只有一个符合子女教育扣除的孩子,并且他们之中既不符合子女教育扣除又不符合赡养老人扣除、只符合子女教育扣除但不符合赡养老人扣除、只符合赡养老人扣除但不符合子女教育扣除、即符合子女教育扣除又符合赡养老人扣除的人数之比是2:1:1:1;此外,他们均不符合其他专项附加扣除.新个税政策下该市的专项附加扣除标准为:住房1000元/月,子女教育每孩1000元/月,赡养老人2000元/月等。
假设该市该收入层级的![]() 从业者都独自享受专项附加扣除,将预估的该市该收入层级的
从业者都独自享受专项附加扣除,将预估的该市该收入层级的![]() 从业者的人均月收入视为其个人月收入.根据样本估计总体的思想,解决如下问题:
从业者的人均月收入视为其个人月收入.根据样本估计总体的思想,解决如下问题:
(1)设该市该收入层级的![]() 从业者2019年月缴个税为
从业者2019年月缴个税为![]() 元,求
元,求![]() 的分布列和期望;
的分布列和期望;
(2)根据新旧个税方案,估计从2019年1月开始,经过多少个月,该市该收入层级的![]() 从业者各月少缴交的个税之和就超过2019年的月收入?
从业者各月少缴交的个税之和就超过2019年的月收入?
【答案】(1)见解析(2)经过12个月,该收入层级的![]() 从业者少缴交的个税的总和就超过2019年的月收入
从业者少缴交的个税的总和就超过2019年的月收入
【解析】
(1)求出4种人群的每月应缴个税额,得出分布列和数学期望;
(2)计算两种政策下的每月应缴个税额度差即可得出结论.
(1)既不符合子女教育扣除也不符合赡养老人扣除的人群每月应纳税所得额为
![]() ,
,
月缴个税![]() ;
;
只符合子女教育扣除但不符合赡养老人扣除的人群每月应纳税所得额为
![]() ,
,
月缴个税![]() ;
;
只符合赡养老人扣除但不符合子女教育扣除的人群每月应纳税所得额为
![]() ,
,
月缴个税![]() ;
;
既符合子女教育扣除又符合赡养老人扣除的人群每月应纳税所得额为
![]() ,
,
月缴个税![]() ;
;
所以![]() 的可能值为2190,1990,1790,1590,
的可能值为2190,1990,1790,1590,
依题意,上述四类人群的人数之比是2:1:1:1,
所以![]() ,
,![]() ,
,
![]() ,
,![]() .,
.,
所以![]() 的分布列为
的分布列为
| 2190 | 1990 | 1790 | 1590 |
|
|
|
|
|
所以![]() ..
..
(2)因为在旧政策下该收入层级的![]() 从业者2019年每月应纳税所得额为
从业者2019年每月应纳税所得额为![]() ,
,
其月缴个税为![]() ,
,
因为在新政策下该收入层级的![]() 从业者2019年月缴个税为1950,
从业者2019年月缴个税为1950,
所以该收入层级的![]() 从业者每月少缴交的个税为
从业者每月少缴交的个税为![]() .,
.,
设经过![]() 个月,该收入层级的
个月,该收入层级的![]() 从业者少缴交的个税的总和就超过24000,
从业者少缴交的个税的总和就超过24000,
则![]() ,因为
,因为![]() ,所以
,所以![]() ,
,
所以经过12个月,该收入层级的![]() 从业者少缴交的个税的总和就超过2019年的月收入.
从业者少缴交的个税的总和就超过2019年的月收入.


科目:高中数学 来源: 题型:
【题目】如图,在四棱锥P-ABCD中,PA⊥底面ABCD,AD⊥AB,AB∥DC,AD=DC=AP=2,AB=1,点E为棱PC的中点.

(1)证明:BE⊥DC;
(2)求直线BE与平面PBD所成角的正弦值;
(3)若F为棱PC上一点,满足BF⊥AC,求二面角F-AB-P的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线![]() 的焦点
的焦点![]() 恰好是椭圆
恰好是椭圆![]() 的右焦点.
的右焦点.
(1)求实数![]() 的值及抛物线
的值及抛物线![]() 的准线方程;
的准线方程;
(2)过点![]() 任作两条互相垂直的直线分别交抛物线
任作两条互相垂直的直线分别交抛物线![]() 于
于![]() 、
、![]() 和
和![]() 、
、![]() 点,求两条弦的弦长之和
点,求两条弦的弦长之和![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了调查民众对国家实行“新农村建设”政策的态度,现通过网络问卷随机调查了年龄在20周岁至80周岁的100人,他们年龄频数分布和支持“新农村建设”人数如下表:
年龄 |
|
|
|
|
|
|
频数 | 10 | 20 | 30 | 20 | 10 | 10 |
支持“新农村建设” | 3 | 11 | 26 | 12 | 6 | 2 |
(1)根据上述统计数据填下面的![]() 列联表,并判断是否有
列联表,并判断是否有![]() 的把握认为以50岁为分界点对“新农村建设”政策的支持度有差异;
的把握认为以50岁为分界点对“新农村建设”政策的支持度有差异;
年龄低于50岁的人数 | 年龄不低于50岁的人数 | 合计 | |
支持 | |||
不支持 | |||
合计 |
(2)现从年龄在![]() 内的5名被调查人中任选两人去参加座谈会,求选出两人中恰有一人支持新农村建设的概率.
内的5名被调查人中任选两人去参加座谈会,求选出两人中恰有一人支持新农村建设的概率.
参考数据:
| 0.150 | 0.100 | 0.050 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 |
参考公式:![]() ,其中
,其中![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在三棱锥P﹣ABC中,AB=1,BC=2,AC![]() ,PC
,PC![]() ,PA
,PA![]() ,PB
,PB![]() ,E是线段BC的中点.
,E是线段BC的中点.
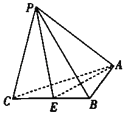
(1)求点C到平面APE的距离d;
(2)求二面角P﹣EA﹣B的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】大学生赵敏利用寒假参加社会实践,对机械销售公司7月份至12月份销售某种机械配件的销售量及销售单价进行了调查,销售单价![]() 和销售量
和销售量![]() 之间的一组数据如下表所示:
之间的一组数据如下表所示:
月份 | 7 | 8 | 9 | 10 | 11 | 12 |
销售单价 | 9 | 9.5 | 10 | 10.5 | 11 | 8 |
销售量 | 11 | 10 | 8 | 6 | 5 | 14 |
(1)根据7至11月份的数据,求出![]() 关于
关于![]() 的回归直线方程;
的回归直线方程;
(2)若由回归直线方程得到的估计数据与剩下的检验数据的误差不超过0.5元,则认为所得到的回归直线方程是理想的,试问(1)中所得到的回归直线方程是否理想?
(3)预计在今后的销售中,销售量与销售单价仍然服从(1)中的关系,若该种机器配件的成本是2.5元/件,那么该配件的销售单价应定为多少元才能获得最大利润?(注:利润=销售收入-成本).
参考公式:回归直线方程![]() ,其中
,其中 ,参考数据:
,参考数据: ![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com