
分析 (1)利用数列中Sn与an关系,先求出an,再由${b}_{n}=\frac{2}{{a}_{n}+1}$化简求出bn;
(2)由题意和(1)求出cn,利用作差法证明结论成立;
(3)由(2)令n=1、2、3分别求出对应的cn,即可求出满足条件的自然数k的最小值.
解答 解:(1)当n=1时,a1=s1=2,
当n≥2时,an=Sn-Sn-1=n2+1-[(n-1)2+1]=2n-1,
所以an=$\left\{\begin{array}{l}{2,n=1}\\{2n-1,n≥2}\end{array}\right.$,
因为${b}_{n}=\frac{2}{{a}_{n}+1}$,所以${b}_{n}=\left\{\begin{array}{l}{\frac{2}{3},n=1}\\{\frac{1}{n},n≥2}\end{array}\right.$;
证明(2)由(1)得,Cn=T2n+1-Tn=bn+1+bn+2+…+b2n+1
=$\frac{1}{n+1}+\frac{1}{n+2}+…+\frac{1}{2n}+\frac{1}{2n+1}$,
所以cn+1-cn=$\frac{1}{2n+3}+\frac{1}{2n+2}-\frac{1}{n+1}$=$\frac{-1}{(2n+3)(2n+2)}$<0,
则cn+1<cn成立,
所以数列{Cn}是单调递减数列;
解:(3)由(2)知:Cn<Cn-1<…<C3<C2<C1,
当n=1时,C1=$\frac{1}{2}+\frac{1}{3}$=$\frac{5}{6}>$$\frac{16}{21}$,
当n=2时,C2=$\frac{1}{3}+\frac{1}{4}+\frac{1}{5}$=$\frac{47}{60}>\frac{16}{21}$,
当n=3时,C3=$\frac{1}{4}+\frac{1}{5}+\frac{1}{6}+\frac{1}{7}$$\frac{319}{420}<\frac{320}{420}$=$\frac{16}{21}$,
当n≥3时,Cn≤C3<$\frac{16}{21}$,
所以自然数k的最小值是3.
点评 本题考查数列与函数、不等式的综合问题,数列中Sn与an关系的应用,考查化简、计算能力,属于中档题.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:选择题
| A. | $\frac{7}{9}$ | B. | -$\frac{5}{6}$ | C. | -$\frac{7}{18}$ | D. | 1 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 已知圆柱OO1底面半径为1,高为π,ABCD是圆柱的一个轴截面.动点M从点B出发沿着圆柱的侧面到达点D,其距离最短时在侧面留下的曲线Γ如图所示.现将轴截面ABCD绕着轴OO1逆时针旋转θ(0<θ≤π)后,边B1C1与曲线Γ相交于点P,设BP的长度为f(θ),则y=f(θ)的图象大致为( )
已知圆柱OO1底面半径为1,高为π,ABCD是圆柱的一个轴截面.动点M从点B出发沿着圆柱的侧面到达点D,其距离最短时在侧面留下的曲线Γ如图所示.现将轴截面ABCD绕着轴OO1逆时针旋转θ(0<θ≤π)后,边B1C1与曲线Γ相交于点P,设BP的长度为f(θ),则y=f(θ)的图象大致为( )| A. |  | B. |  | C. | 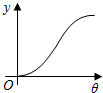 | D. |  |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题

查看答案和解析>>
科目:高中数学 来源: 题型:解答题
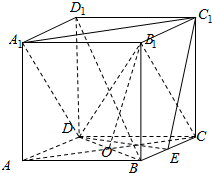 已知正方体ABCD-A1B1C1D1,底面ABCD的中心为O,E为BC的中点,如图
已知正方体ABCD-A1B1C1D1,底面ABCD的中心为O,E为BC的中点,如图查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com