
【题目】已知函数f(x)=![]()
![]() (t+1)lnx,,其中t∈R.
(t+1)lnx,,其中t∈R.
(1)若t=1,求证:当x>1时,f(x)>0成立;
(2)若t>![]() ,判断函数g(x)=x[f(x)+t+1]的零点的个数.
,判断函数g(x)=x[f(x)+t+1]的零点的个数.
【答案】(1)见解析(2)1
【解析】试题分析:(1)当![]() 时,对
时,对![]() 求导,
求导, ![]() 得增区间,
得增区间, ![]() 得减区间,进而求出函数的最小值值,即可证明;(2)若t>
得减区间,进而求出函数的最小值值,即可证明;(2)若t>![]() ,求得函数g(x)=x[f(x)+t+1]的导函数,研究其单调性,根据零点定理再利用导数即可判定零点的个数.
,求得函数g(x)=x[f(x)+t+1]的导函数,研究其单调性,根据零点定理再利用导数即可判定零点的个数.
试题解析:解:(1)t=1时,f(x)=x﹣![]() ﹣2lnx,x>0
﹣2lnx,x>0
∴f′(x)=1+![]() ﹣
﹣![]() =
=![]() =
=![]() ≥0,
≥0,
∴f(x)在(1,+∞)上单调递增,
∴f(x)>f(1)=1﹣1﹣0=0,
∴x>1,f(x)>0成立,
(2)当x∈(0,+∞),g(x)=tx2﹣(t+1)xlnx+(t+1)x﹣1
∴g′(x)=2tx﹣(t+1)lnx,
设m(x)=2tx﹣(t+1)lnx, ∴m′(x)=2t﹣![]() =
=![]() ,
,
令m′(x)=0,得x=![]() ,
,
当0<x<![]() 时,m'(x)<0;当时x>
时,m'(x)<0;当时x>![]() ,m'(x)>0.
,m'(x)>0.
∴g'(x)在(0,![]() )上单调递减,在(
)上单调递减,在(![]() ,+∞)上单调递增.
,+∞)上单调递增.
∴g'(x)的最小值为g′(![]() )=(t+1)(1﹣ln
)=(t+1)(1﹣ln![]() ),
),
∵t>![]() ,∴
,∴![]() =
=![]() +
+![]() <
<![]() +
+![]() <e.
<e.
∴g'(x)的最小值g′(![]() )=(t+1)(1﹣ln
)=(t+1)(1﹣ln![]() )>0,
)>0,
从而,g(x)在区间(0,+∞)上单调递增.
又g(1)=2t>0,又g(![]() )=
)=![]() +
+![]() (6+2lnt)﹣1,
(6+2lnt)﹣1,
设h(t)=e3t﹣(2lnt+6).
则h′(t)=e3﹣![]() .
.
令h'(t)=0得t=![]() .由h'(t)<0,得0<t<
.由h'(t)<0,得0<t<![]() ;
;
由h'(t)>0,得t>![]() .
.
∴h(t)在(0,![]() )上单调递减,在(
)上单调递减,在(![]() ,+∞)上单调递增.
,+∞)上单调递增.
∴h(t)min=h(![]() )=2﹣2ln2>0.
)=2﹣2ln2>0.
∴h(t)>0恒成立.∴e3t>2lnt+6,.
∴g(![]() )<
)<![]() +
+![]() ﹣1=
﹣1=![]() +
+![]() +
+![]() ﹣1<
﹣1<![]() +
+![]() +
+![]() ﹣1<0.
﹣1<0.
∴当t>![]() 时,函数g(x)恰有1个零点
时,函数g(x)恰有1个零点


科目:高中数学 来源: 题型:
【题目】某水果店购进某种水果的成本为![]() ,经过市场调研发现,这种水果在未来30天的销售单价
,经过市场调研发现,这种水果在未来30天的销售单价![]() 与时间
与时间![]() 之间的函数关系式为
之间的函数关系式为![]() ,销售量
,销售量![]() 与时间
与时间![]() 的函数关系式为
的函数关系式为![]() 。
。
(Ⅰ)该水果店哪一天的销售利润最大?最大利润是多少?
(Ⅱ)为响应政府“精准扶贫”号召,该店决定每销售![]() 水果就捐赠
水果就捐赠![]() 元给“精准扶贫”对象.欲使捐赠后不亏损,且利润随时间
元给“精准扶贫”对象.欲使捐赠后不亏损,且利润随时间![]()
![]() 的增大而增大,求捐赠额
的增大而增大,求捐赠额![]() 的值。
的值。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知二次函数![]() 满足
满足![]() (
(![]() ),且
),且![]() .
.
(1)求![]() 的解析式;
的解析式;
(2)若关于![]() 的方程
的方程![]() 在区间
在区间![]() 上有唯一实数根,求实数
上有唯一实数根,求实数![]() 的取值范围(注:相等的实数根算一个).
的取值范围(注:相等的实数根算一个).
(3)函数![]() ,试问是否存在实数
,试问是否存在实数![]() ,使得对任意
,使得对任意![]() ,
, ![]() 都有
都有![]() 成立,若存在,求出实数
成立,若存在,求出实数![]() 的取值范围,若不存在,说明理由.
的取值范围,若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2015男篮亚锦赛决赛阶段,中国男篮以9连胜的不败战绩赢得第28届亚锦赛冠军,同时拿到亚洲唯一1张直通里约奥运会的入场券,赛后,中国男篮主力易建联荣膺本届亚锦赛![]() (最有价值球员),下表是易建联在这9场比赛中投篮的统计数据.
(最有价值球员),下表是易建联在这9场比赛中投篮的统计数据.
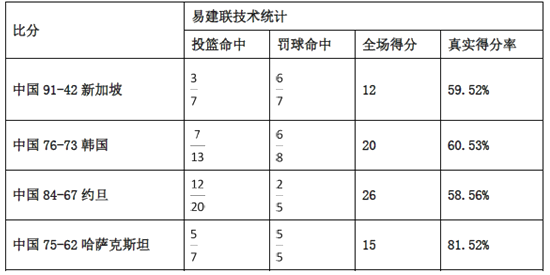
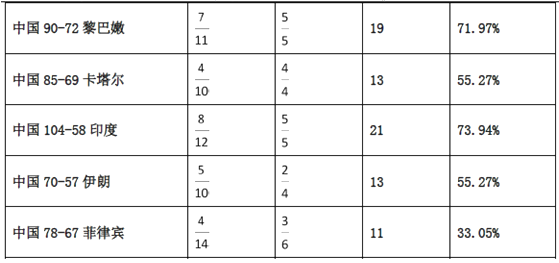
注:(1)表中![]() 表示出手
表示出手![]() 次命中
次命中![]() 次;
次;
(2)![]() (真实得分率)是衡量球员进攻的效率,其计算公式为:
(真实得分率)是衡量球员进攻的效率,其计算公式为:
![]()
![]()
(1)从上述9场比赛中随机选择一场,求易建联在该场比赛中![]() 超过50%的概率;
超过50%的概率;
(2)从上述9场比赛中随机选择一场,求易建联在该场比赛中![]() 至少有一场超过60%的概率;
至少有一场超过60%的概率;
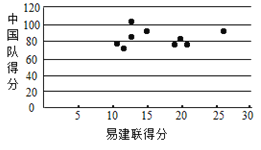
(3)用![]() 来表示易建联某场的得分,用
来表示易建联某场的得分,用![]() 来表示中国队该场的总分,画出散点图如图所示,请根据散点图判断
来表示中国队该场的总分,画出散点图如图所示,请根据散点图判断![]() 与
与![]() 之间是否具有线性相关关系?结合实际简单说明理由.
之间是否具有线性相关关系?结合实际简单说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知某射击运动员每次击中目标的概率都是0.8.现采用随机模拟的方法估计该运动员射击4次,至多击中1次的概率:先由计算器产生0到9之间取整数值的随机数,指定0,1表示没有击中目标,2,3,4,5,6,7,8,9表示击中目标;因为射击4次,故以每4个随机数为一组,代表射击4次的结果.经随机模拟产生了20组随机数:
5 727 0 293 7 140 9 857 0 347
4 373 8 636 9 647 1 417 4 698
0 371 6 233 2 616 8 045 6 011
3 661 9 597 7 424 6 710 4 281
据此估计,该射击运动员射击4次至多击中1次的概率为( )
A. 0.95 B. 0.1
C. 0.15 D. 0.05
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知某运动员每次投篮命中的概率为40%.现采用随机模拟的方法估计该运动员三次投篮恰有两次命中的概率:先由计算器算出0到9之间取整数值的随机数,指定1,2,3,4表示命中,5,6,7,8,9,0表示没有命中;再以每三个随机数为一组,代表三次投篮的结果.经随机模拟产生了20组随机数:
907 966 191 925 271 932 812 458 569 683 431 257 393 027 556 488 730 113 537 989
据此估计,该运动员三次投篮恰有两次命中的概率为( )
A. 0.35 B. 0.25
C. 0,20 D. 0.15
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一个学生在一次竞赛中要回答![]() 道题是这样产生的:从
道题是这样产生的:从![]() 道物理题中随机抽取
道物理题中随机抽取![]() 道;从
道;从![]() 道化学题中随机抽取
道化学题中随机抽取![]() 道;从
道;从![]() 道生物题中随机抽取
道生物题中随机抽取![]() 道.使用合适的方法确定这个学生所要回答的三门学科的题的序号(物理题的编号为
道.使用合适的方法确定这个学生所要回答的三门学科的题的序号(物理题的编号为![]() ,化学题的编号为
,化学题的编号为![]() ,生物题的编号为
,生物题的编号为![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公司试销某种“上海世博会”纪念品,每件按30元销售,可获利50%,设每件纪念品的成本为a元.
(1)试求a的值;
(2)公司在试销过程中进行了市场调查,发现销售量y(件)与每件售价x(元)满足关系y=-10x+800.设每天销售利润为W(元),求每天销售利润W(元)与每件售价x(元)之间的函数解析式;当每件售价为多少时,每天获得的利润最大?最大利润是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com