已知二次函数f(x)满足条件f(0)=1,及f(x+1)-f(x)=2x.
(1)求函数f(x)的解析式;
(2)在区间[-1,1]上,y=f(x)的图象恒在y=2x+m的图象上方,试确定实数m的取值范围.
解:(1)令x=0,则∵f(x+1)-f(x)=2x,
∴f(1)-f(0)=0,
∴f(1)=f(0)
∵f(0)=1
∴f(1)=1,
∴二次函数图象的对称轴为

.
∴可令二次函数的解析式为f(x)=

.
令x=-1,则∵f(x+1)-f(x)=2x,
∴f(0)-f(-1)=-2
∵f(0)=1
∴f(-1)=3,
∴
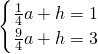
∴a=1,
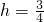
∴二次函数的解析式为
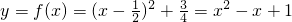
(2)∵在区间[-1,1]上,y=f(x)的图象恒在y=2x+m的图象上方
∴x
2-x+1>2x+m在[-1,1]上恒成立
∴x
2-3x+1>m在[-1,1]上恒成立
令g(x)=x
2-3x+1,则g(x)=(x-

)
2-

∴g(x)=x
2-3x+1在[-1,1]上单调递减
∴g(x)
min=g(1)=-1,
∴m<-1
分析:(1)根据二次函数f(x)满足条件f(0)=1,及f(x+1)-f(x)=2x,可求f(1)=1,f(-1)=3,从而可求函数f(x)的解析式;
(2)在区间[-1,1]上,y=f(x)的图象恒在y=2x+m的图象上方,等价于x
2-x+1>2x+m在[-1,1]上恒成立,等价于x
2-3x+1>m在[-1,1]上恒成立,求出左边函数的最小值,即可求得实数m的取值范围.
点评:本题重点考查二次函数解析式的求解,考查恒成立问题的处理,解题的关键是将在区间[-1,1]上,y=f(x)的图象恒在y=2x+m的图象上方,转化为x
2-3x+1>m在[-1,1]上恒成立.

 .
. .
.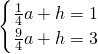
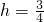
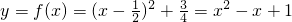
 )2-
)2-


 优百分课时互动系列答案
优百分课时互动系列答案 开心蛙状元作业系列答案
开心蛙状元作业系列答案