
ЁОЬтФПЁПЖдгкСНИіЖЈвхгђЯрЭЌЕФКЏЪ§fЃЈxЃЉЃЌgЃЈxЃЉЃЌШєДцдкЪЕЪ§mЁЂnЪЙhЃЈxЃЉ=mfЃЈxЃЉ+ngЃЈxЃЉЃЌдђГЦКЏЪ§hЃЈxЃЉЪЧгЩЁАЛљКЏЪ§fЃЈxЃЉЃЌgЃЈxЃЉЁБЩњГЩЕФЃЎ
ЃЈ1ЃЉШєfЃЈxЃЉ=x2+3xКЭИіgЃЈxЃЉ=3x+4ЩњГЩвЛИіХМКЏЪ§hЃЈxЃЉЃЌЧѓhЃЈ2ЃЉЕФжЕЃЛ
ЃЈ2ЃЉШєhЃЈxЃЉ=2x2+3xЉ1гЩКЏЪ§fЃЈxЃЉ=x2+axЃЌgЃЈxЃЉ=x+bЃЈaЁЂbЁЪRЧвabЁй0ЃЉЩњГЩЃЌЧѓa+2bЕФШЁжЕЗЖЮЇЃЛ
ЃЈ3ЃЉРћгУЁАЛљКЏЪ§fЃЈxЃЉ=log4ЃЈ4x+1ЃЉЃЌgЃЈxЃЉ=xЉ1ЁБЩњГЩвЛИіКЏЪ§hЃЈxЃЉЃЌЪЙжЎТњзуЯТСаМўЃКЂйЪЧХМКЏЪ§ЃЛЂкгазюаЁжЕ1ЃЛЧѓКЏЪ§hЃЈxЃЉЕФНтЮіЪНВЂНјвЛВНбаОПИУКЏЪ§ЕФЕЅЕїадЃЈЮоашжЄУїЃЉЃЎ
ЁОД№АИЁП
ЃЈ1ЃЉНтЃКЩшhЃЈxЃЉ=mЃЈx2+3xЃЉ+nЃЈ3x+4ЃЉ=mx2+3ЃЈm+nЃЉx+4nЃЌ
ЁпhЃЈxЃЉЪЧХМКЏЪ§ЃЌЁрm+n=0ЃЌЁрhЃЈ2ЃЉ=4m+4n=0ЃЛ
ЃЈ2ЃЉНтЃКЩшhЃЈxЃЉ=2x2+3xЉ1=mЃЈx2+axЃЉ+nЃЈx+bЃЉ=mx2+ЃЈam+nЃЉx+nb
Ёр 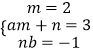 ЕУ
ЕУ 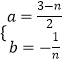
Ёрa+2b= ![]() Љ
Љ ![]() =
= ![]() Љ
Љ ![]() Љ
Љ ![]()
гЩabЁй0жЊЃЌnЁй3ЃЌ
Ёрa+2bЁЪ ![]()
ЃЈ3ЃЉНтЃКЩшhЃЈxЃЉ=mlog4ЃЈ4x+1ЃЉ+nЃЈxЉ1ЃЉ
ЁпhЃЈxЃЉЪЧХМКЏЪ§ЃЌЁрhЃЈЉxЃЉЉhЃЈxЃЉ=0ЃЌ
МДmlog4ЃЈ4Љx+1ЃЉ+nЃЈЉxЉ1ЃЉЉmlog4ЃЈ4x+1ЃЉЉnЃЈxЉ1ЃЉ=0
ЁрЃЈm+2nЃЉx=0ЕУm=Љ2n
дђhЃЈxЃЉ=Љ2nlog4ЃЈ4x+1ЃЉ+nЃЈxЉ1ЃЉ=Љ2n[log4ЃЈ4x+1ЃЉЉ ![]() ]=Љ2n[log4ЃЈ2x+
]=Љ2n[log4ЃЈ2x+ ![]() ЃЉ+
ЃЉ+ ![]() ]
]
ЁпhЃЈxЃЉгазюаЁжЕ1ЃЌдђБигаnЃМ0ЃЌЧвгаЉ2n=1Ёрm=1ЃЎn= ![]()
ЁрhЃЈxЃЉ=log4ЃЈ2x+ ![]() ЃЉ+
ЃЉ+ ![]()
hЃЈxЃЉдк[0ЃЌ+ЁоЃЉЩЯЪЧдіКЏЪ§ЃЌдкЃЈЉЁоЃЌ0]ЩЯЪЧМѕКЏЪ§ЃЎ
ЁОНтЮіЁПЃЈ1ЃЉЯШгУД§ЖЈЯЕЪ§ЗЈБэЪОГіХМКЏЪ§hЃЈxЃЉЃЌдйИљОнЦфЪЧХМКЏЪ§етвЛаджЪЕУЕНв§ШыВЮЪ§ЕФЗНГЬЃЌЧѓГіВЮЪ§ЕФжЕЃЌМДЕУКЏЪ§ЕФНтЮіЪНЃЌДњШыздБфСПЧѓжЕМДПЩЃЎЃЈ2ЃЉЯШгУД§ЖЈЯЕЪ§ЗЈБэЪОГіХМКЏЪ§hЃЈxЃЉЃЌдйИљОнЭЌвЛадНЈСЂв§ШыВЮЪ§ЕФЗНГЬЧѓВЮЪ§ЃЌШЛКѓдйЧѓa+2bЕФШЁжЕЗЖЮЇЃЛЃЈ3ЃЉЯШгУД§ЖЈЯЕЪ§ЗЈБэЪОГіКЏЪ§hЃЈxЃЉЃЌдйИљОнКЏЪ§hЃЈxЃЉЕФаджЪЧѓГіЯрЙиЕФВЮЪ§ЃЌДњШыНтЮіЪНЃЌгЩНтЮібаОПГіЦфЕЅЕїадМДПЩ
ЁОПМЕуОЋЮіЁПИљОнЬтФПЕФвбжЊЬѕМўЃЌРћгУКЏЪ§ЕФЕЅЕїадКЭЦцХМадгыЕЅЕїадЕФзлКЯЕФЯрЙижЊЪЖПЩвдЕУЕНЮЪЬтЕФД№АИЃЌашвЊеЦЮезЂвтЃККЏЪ§ЕФЕЅЕїадЪЧКЏЪ§ЕФОжВПаджЪЃЛКЏЪ§ЕФЕЅЕїадЛЙгаЕЅЕїВЛдіЃЌКЭЕЅЕїВЛМѕСНжжЃЛЦцКЏЪ§дкЙигкдЕуЖдГЦЕФЧјМфЩЯгаЯрЭЌЕФЕЅЕїадЃЛХМКЏЪ§дкЙигкдЕуЖдГЦЕФЧјМфЩЯгаЯрЗДЕФЕЅЕїадЃЎ



| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊКЏЪ§![]() .
.
ЃЈ1ЃЉШєКЏЪ§![]() дкЦфЖЈвхгђФкЮЊдіКЏЪ§ЃЌЧѓЪЕЪ§
дкЦфЖЈвхгђФкЮЊдіКЏЪ§ЃЌЧѓЪЕЪ§![]() ЕФШЁжЕЗЖЮЇЃЛ
ЕФШЁжЕЗЖЮЇЃЛ
ЃЈ3ЃЉЩшКЏЪ§![]() ЃЌШєдк
ЃЌШєдк![]() ЩЯжСЩйДцдквЛЕу
ЩЯжСЩйДцдквЛЕу![]() ЃЌЪЙЕУ
ЃЌЪЙЕУ![]() ГЩСЂЃЌЧѓЪЕЪ§
ГЩСЂЃЌЧѓЪЕЪ§![]() ЕФШЁжЕЗЖЮЇ.
ЕФШЁжЕЗЖЮЇ.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПФГВЭЬќзАаоЃЌашвЊДѓПщНККЯАх![]() еХЃЌаЁПщНККЯАх
еХЃЌаЁПщНККЯАх![]() еХЃЌвбжЊЪаГЁГіЪл
еХЃЌвбжЊЪаГЁГіЪл![]() СНжжВЛЭЌЙцИёЕФНККЯАхЁЃОЙ§ВтЫуЃЌ
СНжжВЛЭЌЙцИёЕФНККЯАхЁЃОЙ§ВтЫуЃЌ ![]() жжЙцИёЕФНККЯАхПЩЭЌЪБНиЕУДѓПщНККЯАх
жжЙцИёЕФНККЯАхПЩЭЌЪБНиЕУДѓПщНККЯАх![]() еХЃЌаЁПщНККЯАх
еХЃЌаЁПщНККЯАх![]() еХЃЌ
еХЃЌ ![]() жжЙцИёЕФНККЯАхПЩЭЌЪБНиЕУДѓПщНККЯАх
жжЙцИёЕФНККЯАхПЩЭЌЪБНиЕУДѓПщНККЯАх![]() еХЃЌаЁПщНККЯАх
еХЃЌаЁПщНККЯАх![]() еХ.вбжЊ
еХ.вбжЊ![]() жжЙцИёНККЯАхУПеХ
жжЙцИёНККЯАхУПеХ![]() дЊЃЌ
дЊЃЌ ![]() жжЙцИёНККЯАхУПеХ
жжЙцИёНККЯАхУПеХ![]() дЊ.ЗжБ№гУ
дЊ.ЗжБ№гУ![]() БэЪОЙКТђ
БэЪОЙКТђ![]() СНжжВЛЭЌЙцИёЕФНККЯАхЕФеХЪ§.
СНжжВЛЭЌЙцИёЕФНККЯАхЕФеХЪ§.
ЃЈ1ЃЉгУ![]() СаГіТњзуЬѕМўЕФЪ§бЇЙиЯЕЪНЃЌВЂЛГіЯргІЕФЦНУцЧјгђЃЛ
СаГіТњзуЬѕМўЕФЪ§бЇЙиЯЕЪНЃЌВЂЛГіЯргІЕФЦНУцЧјгђЃЛ
ЃЈ2ЃЉИљОнЪЉЙЄашЧѓЃЌ ![]() СНжжВЛЭЌЙцИёЕФНККЯАхИїТђЖрЩйеХЛЈЗбзЪН№зюЩйЃПВЂЧѓГізюЩйзЪН№Ъ§.
СНжжВЛЭЌЙцИёЕФНККЯАхИїТђЖрЩйеХЛЈЗбзЪН№зюЩйЃПВЂЧѓГізюЩйзЪН№Ъ§.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПНЋКЏЪ§fЃЈxЃЉ=2sinЃЈ2x+ ![]() ЃЉЕФЭМЯѓЯђгвЦНвЦІеЃЈІеЃО0ЃЉИіЕЅЮЛЃЌдйНЋЭМЯѓЩЯУПвЛЕуКсзјБъЫѕЖЬЕНдРДЕФ
ЃЉЕФЭМЯѓЯђгвЦНвЦІеЃЈІеЃО0ЃЉИіЕЅЮЛЃЌдйНЋЭМЯѓЩЯУПвЛЕуКсзјБъЫѕЖЬЕНдРДЕФ ![]() БЖЃЌЫљЕУЭМЯѓЙигкжБЯпx=
БЖЃЌЫљЕУЭМЯѓЙигкжБЯпx= ![]() ЖдГЦЃЌдђІеЕФзюаЁе§жЕЮЊ ЃЎ
ЖдГЦЃЌдђІеЕФзюаЁе§жЕЮЊ ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЩшКЏЪ§fЃЈxЃЉЕФЖЈвхгђЮЊDЃЌШєДцдкЗЧСуЪЕЪ§mЃЌЪЙЕУЖдгкШЮвтxЁЪMЃЈMDЃЉЃЌгаЃЈxЉmЃЉЁЪDЧвfЃЈxЉmЃЉЁмfЃЈxЃЉЃЌдђГЦfЃЈxЃЉЮЊMЩЯЕФmЖШЕЭЕїКЏЪ§ЃЎШчЙћЖЈвхгђЮЊRЕФКЏЪ§fЃЈxЃЉЪЧЦцКЏЪ§ЃЌЕБxЁн0ЪБЃЌfЃЈxЃЉ=|xЉa2|Љa2 ЃЌ ЧвfЃЈxЃЉЮЊRЩЯЕФ5ЖШЕЭЕїКЏЪ§ЃЌФЧУДЪЕЪ§aЕФШЁжЕЗЖЮЇЮЊ ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊЪ§Са{an}ТњзуЬѕМўЃЈnЉ1ЃЉan+1=ЃЈn+1ЃЉЃЈanЉ1ЃЉЃЌЧвa2=6ЃЌ
ЃЈ1ЃЉМЦЫуa1ЁЂa3ЁЂa4 ЃЌ ЧыВТВтЪ§Са{an}ЕФЭЈЯюЙЋЪНВЂгУЪ§бЇЙщФЩЗЈжЄУїЃЛ
ЃЈ2ЃЉЩшbn=an+nЃЈnЁЪN*ЃЉЃЌЧѓ ![]() ЕФжЕЃЎ
ЕФжЕЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЯТСаУќЬтжаЃЌе§ШЗЕФађКХЪЧ ЃЎ Ђйy=Љ2cosЃЈ ![]() ІаЉ2xЃЉЪЧЦцКЏЪ§ЃЛ
ІаЉ2xЃЉЪЧЦцКЏЪ§ЃЛ
ЂкШєІСЃЌІТЪЧЕквЛЯѓЯоНЧЃЌЧвІСЃОІТЃЌдђsinІСЃОsinІТЃЛ
Ђлx=Љ ![]() ЪЧКЏЪ§y=3sinЃЈ2xЉ
ЪЧКЏЪ§y=3sinЃЈ2xЉ ![]() ЃЉЕФвЛЬѕЖдГЦжсЃЛ
ЃЉЕФвЛЬѕЖдГЦжсЃЛ
ЂмКЏЪ§y=sinЃЈ ![]() Љ2xЃЉЕФЕЅЕїМѕЧјМфЪЧ[kІаЉ
Љ2xЃЉЕФЕЅЕїМѕЧјМфЪЧ[kІаЉ ![]() ЃЌkІа+
ЃЌkІа+ ![]() ]ЃЈkЁЪZЃЉ
]ЃЈkЁЪZЃЉ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊКЏЪ§![]() ЃЌ
ЃЌ ![]() ЃЌЦфжа
ЃЌЦфжа![]() ЃЌ
ЃЌ ![]() .
.
ЃЈ1ЃЉЕБ![]() ЪБЃЌЧѓ
ЪБЃЌЧѓ![]() дкЕу
дкЕу![]() ДІЧаЯп
ДІЧаЯп![]() ЕФЗНГЬЃЛ
ЕФЗНГЬЃЛ
ЃЈ2ЃЉШєКЏЪ§![]() дкЧјМф
дкЧјМф![]() ЩЯЕЅЕїЕндіЃЌЧѓЪЕЪ§
ЩЯЕЅЕїЕндіЃЌЧѓЪЕЪ§![]() ЕФШЁжЕЗЖЮЇЃЛ
ЕФШЁжЕЗЖЮЇЃЛ
ЃЈ3ЃЉМЧ![]() ЃЌЧѓжЄЃК
ЃЌЧѓжЄЃК ![]() .
.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊКЏЪ§y=fЃЈxЃЉЖдгкШЮвтxЁЪRга ![]() ЃЌЧвЕБxЁЪ[Љ1ЃЌ1]ЪБЃЌfЃЈxЃЉ=x2+1ЃЌдђвдЯТУќЬте§ШЗЕФЪЧЃК ЂйКЏЪ§Ъ§y=fЃЈxЃЉЪЧжмЦкЮЊ2ЕФХМКЏЪ§ЃЛ
ЃЌЧвЕБxЁЪ[Љ1ЃЌ1]ЪБЃЌfЃЈxЃЉ=x2+1ЃЌдђвдЯТУќЬте§ШЗЕФЪЧЃК ЂйКЏЪ§Ъ§y=fЃЈxЃЉЪЧжмЦкЮЊ2ЕФХМКЏЪ§ЃЛ
ЂкКЏЪ§y=fЃЈxЃЉдк[2ЃЌ3]ЩЯЕЅЕїЕндіЃЛ
ЂлКЏЪ§ ![]() ЕФзюДѓжЕЪЧ4ЃЛ
ЕФзюДѓжЕЪЧ4ЃЛ
ЂмШєЙигкxЕФЗНГЬ[fЃЈxЃЉ]2ЉfЃЈxЃЉЉm=0гаЪЕИљЃЌдђЪЕЪ§mЕФЗЖЮЇЪЧ[0ЃЌ2]ЃЛ
ЂнЕБx1 ЃЌ x2ЁЪ[1ЃЌ3]ЪБЃЌ ![]() ЃЎ
ЃЎ
ЦфжаецУќЬтЕФађКХЪЧ ЃЎ
ВщПДД№АИКЭНтЮі>>
АйЖШжТаХ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com