
【题目】设x=1与x=2是函数f(x)=aln x+bx2+x的两个极值点.
(1)试确定常数a和b的值;
(2)判断x=1,x=2是函数f(x)的极大值点还是极小值点,并说明理由.
【答案】(1) a=-![]() ,b=-
,b=-![]() .(2)见解析.
.(2)见解析.
【解析】
(1)由题,求出f(x)的导函数f′(x),可知f′(1)=f′(2)=0,解出a,b的值即可;
(2)由(1)可知导函数,再判别出x=1,x=2左右两边导函数的正负,即可判断出是极大值还是极小值.
(1)∵f(x)=aln x+bx2+x,
∴f′(x)=![]() +2bx+1.
+2bx+1.
由极值点的必要条件可知:
f′(1)=f′(2)=0,
∴a+2b+1=0且![]() +4b+1=0,
+4b+1=0,
解方程组得,a=![]() ,b=
,b=![]() .
.
(2)由(1)可知f(x)=![]() ln x
ln x![]() x2+x,
x2+x,
且函数f(x)=![]() ln x
ln x![]() x2+x的定义域是(0,+∞),
x2+x的定义域是(0,+∞),
f′(x)=![]() x-1
x-1![]() x+1=
x+1=![]() .
.
当x∈(0,1)时,f′(x)<0;当x∈(1,2)时,f′(x)>0;
当x∈(2,+∞)时,f′(x)<0;
所以,x=1是函数f(x)的极小值点,
x=2是函数f(x)的极大值点.


 应用题天天练四川大学出版社系列答案
应用题天天练四川大学出版社系列答案科目:高中数学 来源: 题型:
【题目】(1)已知点A,B的坐标分别为(3,0),(-3,0),直线AP,BP相交于点P,且它们的斜率之积是-2,求动点P的轨迹方程.
(2)设P(x,y),直线l1:x+![]() y=0,l2:x-
y=0,l2:x-![]() y=0.若点P到l1的距离与点P到l2的距离之积为2,求动点P的轨迹方程.
y=0.若点P到l1的距离与点P到l2的距离之积为2,求动点P的轨迹方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
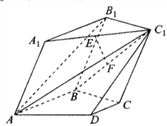
【题目】在如图所示的多面体中,平面![]() 平面
平面![]() ,四边形
,四边形![]() 为边长为2的菱形,
为边长为2的菱形, ![]() 为直角梯形,四边形
为直角梯形,四边形![]() 为平行四边形,且
为平行四边形,且![]() ,
, ![]() ,
, ![]() .
.
(1)若![]() ,
, ![]() 分别为
分别为![]() ,
, ![]() 的中点,求证:
的中点,求证: ![]() 平面
平面![]() ;
;
(2)若![]() ,
, ![]() 与平面
与平面![]() 所成角的正弦值为
所成角的正弦值为![]() ,求二面角
,求二面角![]() 的余弦值.
的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
以平面直角坐标系的原点![]() 为极点,
为极点, ![]() 轴的正半轴为极轴,且两个坐标系取相等的长度单位.已知直线
轴的正半轴为极轴,且两个坐标系取相等的长度单位.已知直线![]() 的参数方程为
的参数方程为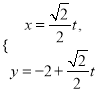 (
(![]() 为参数),曲线
为参数),曲线![]() 的参数方程为
的参数方程为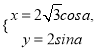 (
(![]() 为参数),曲线
为参数),曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求曲线![]() 和
和![]() 的公共点的极坐标;
的公共点的极坐标;
(2)若![]() 为曲线
为曲线![]() 上的一个动点,求
上的一个动点,求![]() 到直线
到直线![]() 的距离的最大值.
的距离的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】借助计算器填写下表:
|
|
|
|
|
0 | ||||
1 | ||||
10 | ||||
20 | ||||
30 | ||||
50 | ||||
70 | ||||
100 | ||||
150 | ||||
200 | ||||
250 | ||||
300 |
观察表中的变化并归纳各函数递增的规律:
(1)一次函数![]() 与幂函数
与幂函数![]() 之间比较得出的规律;
之间比较得出的规律;
(2)幂函数![]() 与指数函数
与指数函数![]() 之间比较得出的规律;
之间比较得出的规律;
(3)指数函数![]() 与
与![]() 之间比较得出的规律.
之间比较得出的规律.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com