
【题目】已知函数![]() (其中
(其中![]() ),若对任意的
),若对任意的![]() ,
,![]() 恒成立,则实数
恒成立,则实数![]() 的取值范围是________________.
的取值范围是________________.
【答案】![]()
【解析】
判断函数f(x)是R上的奇函数,且是增函数;把f(x2+2)+f(﹣2ax)≥0恒成立化为x2+2≥2ax恒成立,设g(x)=x2﹣2ax+2,利用二次函数的图象与性质,即可求出实数a的取值范围.
函数![]() (其中e≈2.718),x∈R;
(其中e≈2.718),x∈R;
且f(﹣x)=e﹣x﹣ex+ln(﹣x+![]() )=﹣(ex﹣e﹣x)﹣ln(x+
)=﹣(ex﹣e﹣x)﹣ln(x+![]() )=﹣f(x),
)=﹣f(x),
∴f(x)是R上的奇函数,
又f′(x)=ex+e﹣x+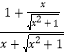 >0恒成立,
>0恒成立,
∴f(x)是定义域R上的单调增函数;
若对任意的x∈[﹣1,2],f(x2+2)+f(﹣2ax)≥0恒成立,
∴f(x2+2)≥﹣f(﹣2ax)恒成立,
∴f(x2+2)≥f(2ax)恒成立,
∴x2+2≥2ax恒成立,
即x2﹣2ax+2≥0在x∈[﹣1,2]上恒成立;
设g(x)=x2﹣2ax+2,其对称轴为x=a,且开口向上;
应满足![]() 或
或![]() 或
或![]() ;
;
解得﹣![]() ≤a<-1或或﹣1≤a≤
≤a<-1或或﹣1≤a≤![]() ;
;
∴实数a的取值范围是﹣![]() ≤a≤
≤a≤![]() .
.
故答案为:﹣![]() ≤a≤
≤a≤![]() .
.


科目:高中数学 来源: 题型:
【题目】已知曲线C1的参数方程是 ![]() (φ为参数),以坐标原点为极点,x轴的非负半轴为极轴建立极坐标系,曲线C2的极坐标系方程是
(φ为参数),以坐标原点为极点,x轴的非负半轴为极轴建立极坐标系,曲线C2的极坐标系方程是 ![]() ,正方形ABCD的顶点都在C1上,且A,B,C,D依逆时针次序排列,点A的极坐标为
,正方形ABCD的顶点都在C1上,且A,B,C,D依逆时针次序排列,点A的极坐标为 ![]() .
.
(1)求点A,B,C,D的直角坐标;
(2)设P为C2上任意一点,求|PA|2+|PB|2+|PC|2+|PD|2的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}的通项公式an=5﹣n,其前n项和为Sn , 将数列{an}的前4项抽去其中一项后,剩下三项按原来顺序恰为等比数列{bn}的前3项,记{bn}的前n项和为Tn , 若存在m∈N* , 使对任意n∈N* , 总有Sn<Tn+λ恒成立,则实数λ的取值范围是( )
A.λ≥2
B.λ>3
C.λ≥3
D.λ>2
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数![]() ,其中
,其中![]() .已知
.已知![]() .
.
(Ⅰ)求![]() .
.
(Ⅱ)将函数![]() 的图象上各点的横坐标伸长为原来的
的图象上各点的横坐标伸长为原来的![]() 倍(纵坐标不变),再将得到的图象向左平移
倍(纵坐标不变),再将得到的图象向左平移![]() 个单位,得到函数
个单位,得到函数![]() 的图象,求
的图象,求![]() 在
在![]() 上的最小值.
上的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】根据市场分析,某蔬菜加工点,当月产量为10吨至25吨时,月生产总成本![]() (万元)可以看出月产量
(万元)可以看出月产量![]() (吨)的二次函数,当月产量为10吨时,月生产成本为20万元,当月产量为15吨时,月生产总成本最低至17.5万元.
(吨)的二次函数,当月产量为10吨时,月生产成本为20万元,当月产量为15吨时,月生产总成本最低至17.5万元.
(I)写出月生产总成本![]() (万元)关于月产量
(万元)关于月产量![]() 吨的函数关系;
吨的函数关系;
(II)已知该产品销售价为每吨1.6万元,那么月产量为多少吨时,可获得最大利润,并求出最大利润.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=ax2+bx+c(a>0,b∈R,c∈R).
(1)若函数f(x)的最小值是f(﹣1)=0,且c=1,求f (2)的值;
(2)若a=1,c=0,且|f(x)|≤1在区间(0,1]上恒成立,试求b的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】雾霾影响人们的身体健康,越来越多的人开始关心如何少产生雾霾,春节前夕,某市健康协会为了了解公众对“适当甚至不燃放烟花爆竹”的态度,随机采访了50人,将凋查情况进行整理后制成下表:
年龄(岁) | [15,25) | [25,35) | [35,45) | [45,55) | [55,65) | [65,75] |
频数 | 5 | 10 | 15 | 10 | 5 | 5 |
赞成人数 | 4 | 6 | 12 | 7 | 3 | 3 |
(1)以赞同人数的频率为概率,若再随机采访3人,求至少有1人持赞同态度的概率;
(2)若从年龄在[15,25),[25,35)的被调查者中各随机选取两人进行追踪调查,记选中的4人中不赞同“适当甚至不燃放烟花爆竹”的人数为X,求随机变量X的分布列和数学期望.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com