
在某校教师趣味投篮比赛中,比赛规则是:每场投6个球,至少投进4个球且最后2个球都投进者获奖;否则不获奖.已知教师甲投进每个球的概率都是 .
.
(Ⅰ)记教师甲在每场的6次投球中投进球的个数为X,求X的分布列及数学期望;
(Ⅱ)求教师甲在一场比赛中获奖的概率.
(Ⅰ)X的分布列
数学期望X 0 1 2 3 4 5 6 P 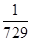

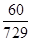
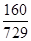
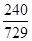
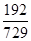
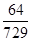
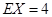 ;(Ⅱ)
;(Ⅱ)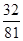 .
.
解析试题分析:(Ⅰ)先定出X的所有可能取值,易知本题是6个独立重复试验中成功的次数的离散概率分布,即为二项分布.由二项分布公式可得到其分布列以及期望.(Ⅱ)根据比赛获胜的规定,教师甲前四次投球中至少有两次投中,后两次必须投中,即可能的情况有1.前四次投中2次(六投四中);2.前四次投中3次(六投五中)3.前四次都投中(六投六中).其中第1种情况有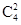 种可能,第2中情况有
种可能,第2中情况有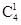 (或
(或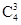 )种可能.将上述三种情况的概率相加即得到教师甲获胜的概率.
)种可能.将上述三种情况的概率相加即得到教师甲获胜的概率.
试题解析:(Ⅰ)X的所有可能取值为0,1,2,3,4,5,6.
依条件可知,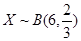
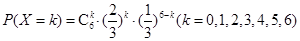 3分
3分
X的分布列为:
6分X 0 1 2 3 4 5 6 P 

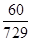
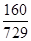
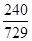
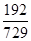
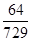
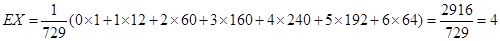 .
.
或因为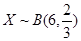 ,所以
,所以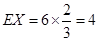 .
.
即 的数学期望为4. 7分
的数学期望为4. 7分
(Ⅱ)设教师甲在一场比赛中获奖为事件A,则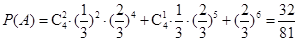 11分
11分
答:教师甲在一场比赛中获奖的概率为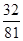 .
.
考点:1.二项分布;2.离散型随机变量的分布列与期望;3.随机事件的概率.


 阳光课堂课时作业系列答案
阳光课堂课时作业系列答案科目:高中数学 来源: 题型:解答题
下图是某市3月1日至14日的空气质量指数趋势图,空气质量指数小于100表示空气质量优良,空气质量指数大于200表示空气重度污染,某人随机选择3月1日至3月13日中的某一天到达该市,并停留2天.
(Ⅰ)求此人到达当日空气重度污染的概率;
(Ⅱ)设X是此人停留期间空气质量优良的天数,求X的分布列与数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
设有关于x的一元二次方程 .
.
(1)若a是从0,1,2,3四个数中任取的一个数,b是从0,1,2三个数中任取的一个数,求上述方程有实根的概率;
(2)若a是从区间[0,3]任取的一个数,b是从区间[0,2]任取的一个数,求上述方程有实根的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
一个口袋中有红球3个,白球4个.
(Ⅰ)从中不放回地摸球,每次摸2个,摸到的2个球中至少有1个红球则中奖,求摸2次恰好第2次中奖的概率;
(Ⅱ)每次同时摸2个,并放回,摸到的2个球中至少有1个红球则中奖,连续摸4次,求中奖次数X的数学期望E(X).
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
其市有小型超市72个,中型超市24个,大型超市12个,现采用分层抽样方法抽取9个超市对其销售商品质量进行调查.
(I)求应从小型、中型、大型超市分别抽取的个数;
(II)若从抽取的9个超市中随机抽取3个做进一步跟踪分析,记随机变量X为抽取的小型超市的个数,求随机变量X的分布列及数学期望E(X) .
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
现有A,B两球队进行友谊比赛,设A队在每局比赛中获胜的概率都是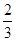 .
.
(Ⅰ)若比赛6局,求A队至多获胜4局的概率;
(Ⅱ)若采用“五局三胜”制,求比赛局数ξ的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某中学作为蓝色海洋教育特色学校,随机抽取100名学生,进行一次海洋知识测试,按测试成绩分组如下:第一组[65,70),第二组 [70,75),第三组[75,80),第四组 [80,85),第五组 [85,90)(假设考试成绩均在[65,90)内),得到频率分布直方图如图:
(1)求测试成绩在[80,85)内的频率;
(2)从第三、四、五组同学中用分层抽样的方法抽取6名同学组成海洋知识宣讲小组,定期在校内进行义务宣讲,并在这6名同学中随机选取2名参加市组织的蓝色海洋教育义务宣讲队,求第四组至少有一名同学被抽中的的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某校学习小组开展“学生语文成绩与外语成绩的关系”的课题研究,对该校高二年级800名学生上学期期末语文和外语成绩,按优秀和不优秀分类得结果:语文和外语都优秀的有60人,语文成绩优秀但外语不优秀的有140人,外语成绩优秀但语文不优秀的有100人.
(Ⅰ)能否在犯错概率不超过0.001的前提下认为该校学生的语文成绩与外语成绩有关系?
(Ⅱ)4名成员随机分成两组,每组2人,一组负责收集成绩,另一组负责数据处理。求学生甲分到负责收集成绩组,学生乙分到负责数据处理组的概率。
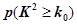 | 0.010 | 0.005 | 0.001 |
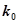 | 6.635 | 7.879 | 10.828 |
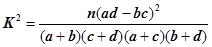
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
为增强市民的节能环保意识,某市面向全市征召义务宣传志愿者.从符合条件的500名志愿者中随机抽取100名志愿者,其年龄频率分布直方图如图所示,其中年龄分组区间是: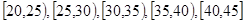 .
.
(I)求图中 的值并根据频率分布直方图估计这500名志愿者中年龄在
的值并根据频率分布直方图估计这500名志愿者中年龄在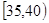 岁的人数;
岁的人数;
(II)在抽出的100名志愿者中按年龄采用分层抽样的方法抽取20名参加中心广场的宣传活动,再从这20名中采用简单随机抽样方法选取3名志愿者担任主要负责人.记这3名志愿者中“年龄低于35岁”的人数为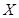 ,求
,求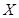 的分布列及数学期望.
的分布列及数学期望. 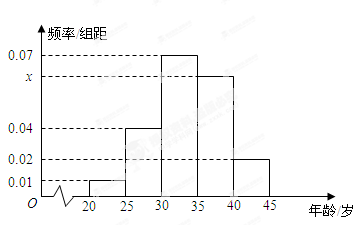
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com