练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】已知直线l1：x+2y+1=0，l2：-2x+y+2=0，它们相交于点A.

    (1)判断直线l1和l2是否垂直？请给出理由.

    (2)求过点A且与直线l3：3x+y+4=0平行的直线方程.

    【答案】（1）l1⊥l2；（2）

    【解析】试题分析：（1）利用两条直线方程，求得两直线的斜率，验证，即可得到结论；

    （2）联立方程组，求得点的坐标，再来平行关系得到直线的斜率，利用点斜式即可求解直线方程.

    试题解析：

    (1)垂直.直线l1的斜率k1=-，直线l2的斜率k2=2，

    因为k1k2=-×2=-1，

    所以l1⊥l2.

    (2)由方程组

    解得点A的坐标为，

    直线l3的斜率为-3，

    所以所求直线方程为：y-=-3，化为一般式得：3x+y-1=0.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】已知函数f（x）=2cos22x﹣2，给出下列命题： ①β∈R，f（x+β）为奇函数；
    ②α∈（0， ），f（x）=f（x+2α）对x∈R恒成立；
    ③x1 ， x2∈R，若|f（x1）﹣f（x2）|=2，则|x1﹣x2|的最小值为 ；
    ④x1 ， x2∈R，若f（x1）=f（x2）=0，则x1﹣x2=kπ（k∈Z）．其中的真命题有（ ）
    A.①②
    B.③④
    C.②③
    D.①④

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，正方体ABCD－A′B′C′D′的棱长为a，连接A′C′，A′D，A′B，BD，BC′，C′D，得到一个三棱锥.求：

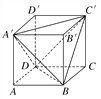
    (1)三棱锥A′－BC′D的表面积与正方体表面积的比值；

    (2)三棱锥A′－BC′D的体积.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，在两块钢板上打孔，用钉帽呈半球形、钉身为圆柱形的铆钉(图1)穿在一起，在没有帽的一端锤打出一个帽，使得与钉帽的大小相等.铆合的两块钢板，成为某种钢结构的配件，其截面图如图2.(单位：mm，加工中不计损失).

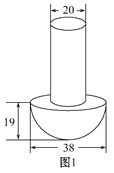
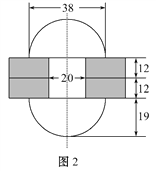
    (1)若钉身高度是钉帽高度的2倍，求铆钉的表面积.

    (2)若每块钢板的厚度为12mm，求钉身的长度(结果精确到1 mm).

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】下图是甲、乙两人在一次射击比赛中中靶的情况(击中靶中心的圆面为10环，靶中各数字表示该数字所在圆环被击中所得的环数)，每人射击了6次．

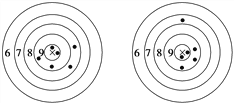
    甲射击的靶　　 乙射击的靶

    (1)请用列表法将甲、乙两人的射击成绩统计出来；

    (2)请你用学过的统计知识，对甲、乙两人这次的射击情况进行比较．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】设命题p：直线mx﹣y+1=0与圆（x﹣2）2+y2=4有公共点；设命题q：实数m满足方程 + =1表示双曲线．
    （1）若“p∧q”为真命题，求实数m的取值范围；
    （2）若“p∧q”为假命题，“p∨q”为真命题，求实数m的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】函数f（x）=是定义在[-l，1]上的奇函数，且f（）=。

    （1）确定函数f（x）的解析式；

    （2）判断并用定义证明f（x）在（-1，1）上的单调性；

    （3）若f（1-3m）+f（1+m）≥0，求实数m的所有可能的取值。

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数，(其中A＞0，ω＞0，0＜φ＜)的图象与x轴的交点中，相邻两个交点之间的距离为，且图象上一个最低点为M(，－2)．

    （1）求f(x)的解析式；

    （2）将函数f(x)的图象向右平移个单位后，再将所得图象上各点的横坐标缩小到原来的，纵坐标不变，得到y＝g(x)的图象，求函数y＝g(x)的解析式．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，四棱锥S—ABCD的底面为正方形，SD⊥底面ABCD，则下列结论

    ①AC⊥SB

    ②AB∥平面SCD

    ③SA与平面ABD所成的角等于SC与平面ABD所成的角

    ④AB与SC所成的角等于DC与SA所成的角．

    ⑤二面角的大小为

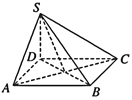
    其中，正确结论的序号是________.

    查看答案和解析>>

    同步练习册答案