
【题目】已知函数f(x)=lg(ax﹣bx)(a>1>b>0).
(1)求f(x)的定义域;
(2)若f(x)在(1,+∞)上递增且恒取正值,求a,b满足的关系式.
【答案】
(1)解:∵ax﹣bx>0,
∴( ![]() )x>1,
)x>1,
∵a>1>b>0
∴x>0,
即f(x)的定义域为(0,+∞)
(2)解:因为f(x)是增函数,所以当x∈(1,+∞)时,f(x)>f(1),
∴只需f(1)=lg(a﹣b)≥0,
∴a﹣b≥1
【解析】(1)要求ax﹣bx>0,转换为( ![]() )x>1,利用指数函数性质求解;(2)由增函数可得f(x)>f(1),只需f(1)=lg(a﹣b)≥0即可.
)x>1,利用指数函数性质求解;(2)由增函数可得f(x)>f(1),只需f(1)=lg(a﹣b)≥0即可.
【考点精析】本题主要考查了函数的定义域及其求法的相关知识点,需要掌握求函数的定义域时,一般遵循以下原则:①![]() 是整式时,定义域是全体实数;②
是整式时,定义域是全体实数;②![]() 是分式函数时,定义域是使分母不为零的一切实数;③
是分式函数时,定义域是使分母不为零的一切实数;③![]() 是偶次根式时,定义域是使被开方式为非负值时的实数的集合;④对数函数的真数大于零,当对数或指数函数的底数中含变量时,底数须大于零且不等于1,零(负)指数幂的底数不能为零才能正确解答此题.
是偶次根式时,定义域是使被开方式为非负值时的实数的集合;④对数函数的真数大于零,当对数或指数函数的底数中含变量时,底数须大于零且不等于1,零(负)指数幂的底数不能为零才能正确解答此题.


科目:高中数学 来源: 题型:
【题目】石家庄市为鼓励居民节约用电,采用分段计费的方法计算电费,每月用电不超过100度时,按每度0.52元计算,每月用电量超过100度时,其中的100度仍按原标准收费,超过的部分每度按0.6元计算.
(1)设月用电x度时,应缴电费y元,写出y关于x的函数关系式;
(2)小明家第一季度缴纳电费情况如表:
月份 | 一月 | 二月 | 三月 | 合计 |
缴费金额 | 82元 | 64元 | 46.8元 | 192.8元 |
问小明家第一季度共用电多少度?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知双曲线C: ![]() 的离心率是
的离心率是 ![]() ,其一条准线方程为x=
,其一条准线方程为x= ![]() .
.
(Ⅰ)求双曲线C的方程;
(Ⅱ)设双曲线C的左右焦点分别为A,B,点D为该双曲线右支上一点,直线AD与其左支交于点E,若 ![]() =λ
=λ ![]() ,求实数λ的取值范围.
,求实数λ的取值范围.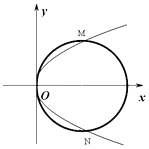
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某租赁公司拥有汽车100辆.当每辆车的月租金为3000元时,可全部租出,当每辆车的月租金每增加50元时,未租出的车将会增加一辆,租出的车每辆每月需要维护费150元,未租出的车每辆每月需要维护费50元.,当每辆车的月租金定为x元时,租赁公司的月收益为y元,
(1)试写出x,y的函数关系式(不要求写出定义域);
(2)租赁公司某月租出了88辆车,求租赁公司的月收益多少元?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】中央政府为了应对因人口老龄化而造成的劳动力短缺等问题,拟定出台“延迟退休年龄政策”,为了了解人们对“延迟退休年龄政策”的态度,责成人社部进行调研,人社部从网上年龄在![]() 岁的人群中随机调查100人,调查数据的频率分布直方图和支持“延迟退休”的人数与年龄的统计结果如下:
岁的人群中随机调查100人,调查数据的频率分布直方图和支持“延迟退休”的人数与年龄的统计结果如下:
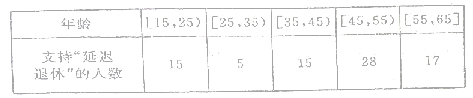
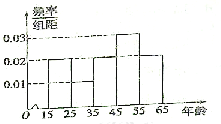
(1)由以上统计数据填![]() 列联表,并判断是否95%的把握认为以
列联表,并判断是否95%的把握认为以![]() 岁为界点的不同人群对“延迟退休年龄政策”的支持有差异;
岁为界点的不同人群对“延迟退休年龄政策”的支持有差异;

(2)若以![]() 岁为分界点,从不支持“延迟退休”的人中按分层抽样的方法抽取
岁为分界点,从不支持“延迟退休”的人中按分层抽样的方法抽取![]() 人参加某项活动,现从这
人参加某项活动,现从这![]() 人中随机抽
人中随机抽![]() 人.
人.
①抽到![]() 人是
人是![]() 岁以下时,求抽到的另一人是
岁以下时,求抽到的另一人是![]() 岁以上的概率;
岁以上的概率;
②记抽到![]() 岁以上的人数为
岁以上的人数为![]() ,求随机变量
,求随机变量![]() 的分布列及数学期望.
的分布列及数学期望.
|
|
|
|
|
|
|
|
|
|
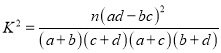
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如果一个几何体的主视图与左视图都是全等的长方形,边长分别是4cm与2cm如图所示,俯视图是一个边长为4cm的正方形. 
(1)求该几何体的全面积.
(2)求该几何体的外接球的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知集合A={x|x2﹣3x﹣10≤0},B={x|m﹣4≤x≤3m+2}.
(1)若A∪B=B,求实数m的取值范围;
(2)若A∩B=B,求实数m的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com