
 如图l,等腰梯形ABCD中,AD∥BC,AB=AD,∠ABC=60°,E是BC的中点.如图2,将△ABE沿AE折起,使二面角B-AE-C成直二面角,连接BC,BD,P是棱BC的中点.
如图l,等腰梯形ABCD中,AD∥BC,AB=AD,∠ABC=60°,E是BC的中点.如图2,将△ABE沿AE折起,使二面角B-AE-C成直二面角,连接BC,BD,P是棱BC的中点. (1)证明:连接BD,取AE中点M,连接BM,DM.
(1)证明:连接BD,取AE中点M,连接BM,DM. ),D(0,
),D(0, ,0),C(2,
,0),C(2, ,0)
,0) ,
, ,
,





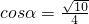
 ),D(0,
),D(0, ,0),C(2,
,0),C(2, ,0),故
,0),故 ,
, ,
, ,可求平面BCD的法向量,从而可求直线EB与平面BCD所成的角的余弦值.
,可求平面BCD的法向量,从而可求直线EB与平面BCD所成的角的余弦值.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:

查看答案和解析>>
科目:高中数学 来源: 题型:
 如图l,等腰梯形ABCD中,AD∥BC,AB=AD,∠ABC=60°,E是BC的中点.如图2,将△ABE沿AE折起,使二面角B-AE-C成直二面角,连接BC,BD,P是棱BC的中点.
如图l,等腰梯形ABCD中,AD∥BC,AB=AD,∠ABC=60°,E是BC的中点.如图2,将△ABE沿AE折起,使二面角B-AE-C成直二面角,连接BC,BD,P是棱BC的中点.查看答案和解析>>
科目:高中数学 来源: 题型:
(09年江宁中学三月)(14分)如图l,等腰梯形ABCD中,AD∥BC,AB=AD,∠ABC=600,E是BC的中点.如图2,将△ABE沿AE折起,使二面角B―AE―C成直二面角,连结BC,BD,F是CD的中点,P是棱BC的中点.
![]() (1)求证:AE⊥BD;(4分) ’
(1)求证:AE⊥BD;(4分) ’
![]() (2)求证:平面PEF⊥平面AECD;(6分)
(2)求证:平面PEF⊥平面AECD;(6分)
![]() (3)判断DE能否垂直于平面ABC?并说明理由.(4分)
(3)判断DE能否垂直于平面ABC?并说明理由.(4分)
![]()

![]()
查看答案和解析>>
科目:高中数学 来源: 题型:解答题

查看答案和解析>>
科目:高中数学 来源:2011-2012学年山西省运城市临猗中学高二(上)周考数学试卷(8)(理科)(解析版) 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com