
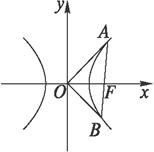
解析:设A、B两点的坐标分别为(x1,y1)、(x2,y2),双曲线x2-![]() =1的右焦点为F(2,0),因此,直线AB过点(2,0),当直线AB垂直于x轴时,把x1=x2=2代入双曲线方程,得y1=3,y2=-3,此时OA不垂直于OB,不合题意;当AB不垂直于x轴时,设其斜率为k,方程为y=k(x-2),代入双曲线方程,整理得(3-k2)x2+4k2x-4k2-3=0,∴x1x2=
=1的右焦点为F(2,0),因此,直线AB过点(2,0),当直线AB垂直于x轴时,把x1=x2=2代入双曲线方程,得y1=3,y2=-3,此时OA不垂直于OB,不合题意;当AB不垂直于x轴时,设其斜率为k,方程为y=k(x-2),代入双曲线方程,整理得(3-k2)x2+4k2x-4k2-3=0,∴x1x2=![]() ,x1+x2=
,x1+x2=![]() . ①
. ①
∴y1y2=k(x1-2)·k(x2-2)=k2[x1x2-2(x1+x2)+4].∵OA⊥OB,∴![]() =-1(显然x1≠0,x2≠0),
=-1(显然x1≠0,x2≠0),
即x1x2+y1y2=0.∴x1x2+k2[x1x2-2(x1+x2)+4]=0,把①式代入得(k2+1)·![]() -2k2·
-2k2·![]() +4k2=0,
+4k2=0,
解得k2=![]() ,k=±
,k=±![]() ,因此,所求直线方程为y=±
,因此,所求直线方程为y=±![]() (x-2).
(x-2).


 夺冠金卷全能练考系列答案
夺冠金卷全能练考系列答案科目:高中数学 来源: 题型:
 以O为原点,
以O为原点,| OA |
| OA |
| AG |
| OG |
查看答案和解析>>
科目:高中数学 来源: 题型:
 (2008•宣武区一模)在面积为9的△ABC中,tan∠BAC=-
(2008•宣武区一模)在面积为9的△ABC中,tan∠BAC=-| 4 |
| 3 |
| CD |
| DB |
| DE |
| DF |
查看答案和解析>>
科目:高中数学 来源: 题型:
(08年宣武区质量检一)(14分)
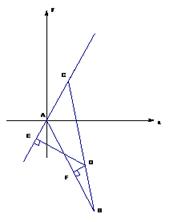
在面积为9的![]() 中,
中,![]() ,且
,且![]() 。现建立以A点为坐标原点,以
。现建立以A点为坐标原点,以![]() 的平分线所在直线为x轴的平面直角坐标系,如图所示。
的平分线所在直线为x轴的平面直角坐标系,如图所示。
(1) 求AB、AC所在的直线方程;
(2) 求以AB、AC所在的直线为渐近线且过点D的
双曲线的方程;
(3) 过D分别作AB、AC所在直线的垂线DF、DE
(E、F为垂足),求![]() 的值。
的值。

查看答案和解析>>
科目:高中数学 来源: 题型:
(08年鄞州中学模拟理)(15分) 在面积为9的![]() 中,
中,![]() ,且
,且![]() 。现建立以A点为坐标原点,以
。现建立以A点为坐标原点,以![]() 的平分线所在直线为x轴的平面直角坐标系,如图所示。
的平分线所在直线为x轴的平面直角坐标系,如图所示。
(1) 求AB、AC所在的直线方程;
(2) 求以AB、AC所在的直线为渐近线且过点D的双曲线的方程;
(3)过D分别作AB、AC所在直线的垂线DF、DE(E、F为垂足),求![]() 的值。
的值。

查看答案和解析>>
科目:高中数学 来源: 题型:
在面积为9的![]() 中,
中,![]() ,且
,且![]() 。现建立以A点为坐标原点,以
。现建立以A点为坐标原点,以![]() 的平分线所在直线为x轴的平面直角坐标系,如图所示。
的平分线所在直线为x轴的平面直角坐标系,如图所示。
(1)求AB、AC所在的直线方程;
(2)求以AB、AC所在的直线为渐近线且过点D的双曲线的方程;
(3)过D分别作AB、AC所在直线的垂线DF、DE(E、F为垂足),求![]() 的值。
的值。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com