
【题目】设![]()
(1)求![]() 在
在![]() 上的最大值和最小值;
上的最大值和最小值;
(2)把![]() 的图像上的所有点的横坐标伸长到原来的2倍(纵坐标不变),再把得到的图像向左平移
的图像上的所有点的横坐标伸长到原来的2倍(纵坐标不变),再把得到的图像向左平移![]() 个单位长度,得到函数
个单位长度,得到函数![]() 的图像,求
的图像,求![]() 的单调减区间
的单调减区间
科目:高中数学 来源: 题型:
【题目】已知各项均不相等的等差数列{an}的前n项和为Sn,若S3=15,且a3+1为a1+1和a7+1的等比中项.
(1)求数列{an}的通项公式与前n项和Sn;
(2)设Tn为数列{![]() }的前n项和,问是否存在常数m,使Tn=m[
}的前n项和,问是否存在常数m,使Tn=m[![]() +
+![]() ],若存在,求m的值;若不存在,说明理由.
],若存在,求m的值;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列说法正确的是( )
A.两条相交直线在同一平面内的射影必为相交直线
B.不共线三点到平面![]() 的距离相等,则这三点确定的平面不一定与平面
的距离相等,则这三点确定的平面不一定与平面![]() 平行
平行
C.对确定的两异面直线,过空间任一点有且只有一个平面与两异面直线都平行
D.两个相交平面的交线是一条线段
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,椭圆C:![]() 的右准线方程为x=2,且两焦点与短轴的一个顶点构成等腰直角三角形.
的右准线方程为x=2,且两焦点与短轴的一个顶点构成等腰直角三角形.
(1)求椭圆C的方程;
(2)假设直线l:![]() 与椭圆C交于A,B两点.①若A为椭圆的上顶点,M为线段AB中点,连接OM并延长交椭圆C于N,并且
与椭圆C交于A,B两点.①若A为椭圆的上顶点,M为线段AB中点,连接OM并延长交椭圆C于N,并且![]() ,求OB的长;②若原点O到直线l的距离为1,并且
,求OB的长;②若原点O到直线l的距离为1,并且![]() ,当
,当![]() 时,求△OAB的面积S的范围.
时,求△OAB的面积S的范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】当我们所处的北半球为冬季的时候,新西兰的惠灵顿市恰好是盛夏,因此北半球的人们冬天愿意去那里旅游,下面是一份惠灵顿机场提供的月平均气温统计表.
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 17.3 | 17.9 | 17.3 | 15.8 | 13.7 | 11.6 | 10.06 | 9.5 | 10.06 | 11.6 | 13.7 | 15.8 |
(1)根据这个统计表提供的数据,为惠灵顿市的月平均气温作出一个函数模型;
(2)当自然气温不低于13.7℃时,惠灵顿市最适宜旅游,试根据你所确定的函数模型,确定惠灵顿市的最佳旅游时间.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某市有![]() ,
,![]() 两家乒乓球俱乐部,两家的设备和服务都很好,但收费标准不同,
两家乒乓球俱乐部,两家的设备和服务都很好,但收费标准不同,![]() 俱乐部每张球台每小时5元,
俱乐部每张球台每小时5元,![]() 俱乐部按月收费,一个月中
俱乐部按月收费,一个月中![]() 以内(含
以内(含![]() )每张球台90元,超过
)每张球台90元,超过![]() 的部分每张球台每小时加收2元.某学校准备下个月从这两家中的一家租一张球台开展活动,其活动时间不少于
的部分每张球台每小时加收2元.某学校准备下个月从这两家中的一家租一张球台开展活动,其活动时间不少于![]() ,也不超过
,也不超过![]() .
.
(1)设在![]() 俱乐部租一-张球台开展活动
俱乐部租一-张球台开展活动![]() 的收费为
的收费为![]() 元
元![]() ,在
,在![]() 俱乐部租一张球台开展活动
俱乐部租一张球台开展活动![]() 的收费为
的收费为![]() 元
元![]() ,试求
,试求![]() 和
和![]() 的解析式;
的解析式;
(2)问选择哪家俱乐部比较合算?为什么?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,AB是圆的直径,PA垂直圆所在的平面,C是圆上的点.
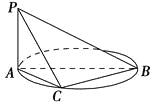
(1)求证:平面PAC⊥平面PBC;
(2)若AB=2,AC=1,PA=1,求二面角C-PB-A的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】给出下列命题:
①命题“若![]() ,则方程
,则方程![]() 无实根”的否命题;
无实根”的否命题;
②命题“在![]() 中,
中,![]() ,那么
,那么![]() 为等边三角形”的逆命题;
为等边三角形”的逆命题;
③命题“若![]() ,则
,则![]() ”的逆否命题;
”的逆否命题;
④“若![]() ,则
,则![]() 的解集为
的解集为![]() ”的逆命题;
”的逆命题;
其中真命题的序号为( )
A.①②③④B.①②④C.②④D.①②③
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com