Question

圆：x²+y²-4x+6y=0和圆：x²+y²-6x=0交于A，B两点，则AB的垂直平分线的方程是________．

Answer 1

3x-y-9=0
分析：现根据两个圆的方程求出圆心的坐标，由题意可得AB的垂直平分线的方程就是两圆的圆心所在的直线的方程，由两点式求得AB的垂直平分线的方程，再化为一般式．
解答：圆：x²+y²-4x+6y=0 的圆心坐标为（2，-3），圆：x²+y²-6x=0的圆心坐标为（3，0），
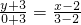
由题意可得AB的垂直平分线的方程就是两圆的圆心所在的直线的方程，由两点式求得AB的垂直平分线的方程是 ，即3x-y-9=0，
故答案为 3x-y-9=0．
点评：本题主要考查用两点式求直线方程的方法，判断AB的垂直平分线的方程就是两圆的圆心所在的直线的方程，是解题的关键，属于基础题．