
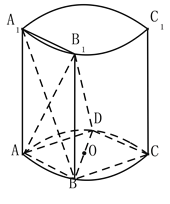
【题目】如图,在圆柱中,A,B,C,D是底面圆的四等分点,O是圆心,A1A,B1B,C1C与底面ABCD垂直,底面圆的直径等于圆柱的高.
(Ⅰ)证明:BC⊥AB1;
(Ⅱ)(ⅰ)求二面角A1 - BB1 - D的大小;
(ⅱ)求异面直线AB1和BD所成角的余弦值.
【答案】(Ⅰ)见解析;(Ⅱ)(ⅰ) ![]() ;(ⅱ)
;(ⅱ) ![]() .
.
【解析】试题分析:(Ⅰ)由已知条件先证明BC⊥平面A1B1BA,又BA1![]() 平面A1B1BA,所以BC⊥AB1.
平面A1B1BA,所以BC⊥AB1.
(Ⅱ)(ⅰ)由圆柱性质知CB、CD、CC1两两垂直.以C为原点,以![]() 、
、![]() 、
、![]() 为x轴、y轴、z轴正方向建系求解即可;
为x轴、y轴、z轴正方向建系求解即可;
(ⅱ)通过求向量![]() ,
, ![]() 的夹角,可得异面直线AB1和BD所成角的余弦值.
的夹角,可得异面直线AB1和BD所成角的余弦值.
试题解析:(Ⅰ)证明:因为B1B⊥平面ABCD,且BC![]() 平面ABCD,所以BC⊥B1B,又因为在底面圆O中,AB⊥BC,AB∩B1B = B,所以BC⊥平面A1B1BA,又因为BA1
平面ABCD,所以BC⊥B1B,又因为在底面圆O中,AB⊥BC,AB∩B1B = B,所以BC⊥平面A1B1BA,又因为BA1![]() 平面A1B1BA,所以BC⊥AB1.
平面A1B1BA,所以BC⊥AB1.
(Ⅱ)(ⅰ)由圆柱性质知CB、CD、CC1两两垂直.以C为原点,以![]() 、
、![]() 、
、![]() 为x轴、y轴、z轴正方向建立空间直角坐标系
为x轴、y轴、z轴正方向建立空间直角坐标系![]() ,不妨设圆柱的高为2.
,不妨设圆柱的高为2.
则![]() ,
, ![]() ,
, ![]() .所以平面A1B1B的一个法向量是
.所以平面A1B1B的一个法向量是![]() .
.
平面BB1D的一个法向量是![]() .
.
所以 .
.
由图知二面角A1 - BB1 - D是锐二面角,所以它的大小是![]() .
.
(ⅱ)由题意得![]() ,
, ![]() ,
, ![]() .
.
所以![]() ,
, ![]() .
.
所以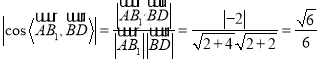 .
.


 中考利剑中考试卷汇编系列答案
中考利剑中考试卷汇编系列答案 教育世家状元卷系列答案
教育世家状元卷系列答案 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案科目:高中数学 来源: 题型:
【题目】某单位共有10名员工,他们某年的收入如下表:
员工编号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
年薪(万元) | 4 | 4.5 | 6 | 5 | 6.5 | 7.5 | 8 | 8.5 | 9 | 51 |
(1)求该单位员工当年年薪的平均值和中位数;
(2)从该单位中任取2人,此2人中年薪收入高于7万的人数记为![]() ,求
,求![]() 的分布列和期望;
的分布列和期望;
(3)已知员工年薪收入与工作年限成正相关关系,某员工工作第一年至第四年的年薪分别为4万元,5.5万元,6万元,8.5万元,预测该员工第五年的年薪为多少?
附:线性回归方程![]() 中系数计算公式分别为:
中系数计算公式分别为:
 ,
, ![]() ,其中
,其中![]() 为样本均值.
为样本均值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知全集U=R,集合A={x|2x+a>0},B={x|x2﹣2x﹣3>0}. (Ⅰ)当a=2时,求集合A∩B;
(Ⅱ)若A∩(UB)=,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4—4:坐标系与参数方程
在平面直角坐标系xOy中,曲线C1的参数方程为![]() (t为参数).在以坐标原点为极点,x轴正半轴为极轴的极坐标系中,曲线C2:
(t为参数).在以坐标原点为极点,x轴正半轴为极轴的极坐标系中,曲线C2: ![]() .
.
(Ⅰ)求曲线C1和C2的直角坐标方程,并分别指出其曲线类型;
(Ⅱ)试判断:曲线C1和C2是否有公共点?如果有,说明公共点的个数;如果没有,请说明理由;
(Ⅲ)设![]() 是曲线C1上任意一点,请直接写出a + 2b的取值范围.
是曲线C1上任意一点,请直接写出a + 2b的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设G为△ABC的重心,过G作直线l分别交线段AB,AC(不与端点重合)于P,Q.若 ![]() =λ
=λ ![]() ,
, ![]() =μ
=μ ![]()
(1)求 ![]() +
+ ![]() 的值;
的值;
(2)求λμ的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点![]() ,点
,点![]() 是圆
是圆![]() 上的任意一点,,线段
上的任意一点,,线段![]() 的垂直平分线与直线
的垂直平分线与直线![]() 交于点
交于点![]() .
.
(1)求![]() 点的轨迹方程;
点的轨迹方程;
(2)若直线![]() 与点
与点![]() 的轨迹相切,且与圆
的轨迹相切,且与圆![]() 相交于点
相交于点![]() 和
和![]() ,求直线
,求直线![]() 和三角形
和三角形![]() 的面积.
的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,其中
,其中![]() .
.
(Ⅰ) 当a=-1时,求证: ![]() ;
;
(Ⅱ) 对任意![]() ,存在
,存在![]() ,使
,使![]() 成立,求a的取值范围.(其中e是自然对数的底数,e=2.71828…)
成立,求a的取值范围.(其中e是自然对数的底数,e=2.71828…)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com