
【题目】已知a≥3,函数F(x)=min{2|x﹣1|,x2﹣2ax+4a﹣2},其中min(p,q)= ![]()
(1)求使得等式F(x)=x2﹣2ax+4a﹣2成立的x的取值范围
(2)(i)求F(x)的最小值m(a)
(ii)求F(x)在[0,6]上的最大值M(a)
【答案】
(1)解:由a≥3,故x≤1时,
x2﹣2ax+4a﹣2﹣2|x﹣1|=x2+2(a﹣1)(2﹣x)>0;
当x>1时,x2﹣2ax+4a﹣2﹣2|x﹣1|=x2﹣(2+2a)x+4a=(x﹣2)(x﹣2a),
则等式F(x)=x2﹣2ax+4a﹣2成立的x的取值范围是[2,2a];
(2)解:(i)设f(x)=2|x﹣1|,g(x)=x2﹣2ax+4a﹣2,
则f(x)min=f(1)=0,g(x)min=g(a)=﹣a2+4a﹣2.
由﹣a2+4a﹣2=0,解得a=2+ ![]() (负的舍去),
(负的舍去),
由F(x)的定义可得m(a)=min{f(1),g(a)},
即m(a)= ![]() ;
;
(ii)当0≤x≤2时,F(x)≤f(x)≤max{f(0),f(2)}=2=F(2);
当2<x≤6时,F(x)≤g(x)≤max{g(2),g(6)}
=max{2,34﹣8a}=max{F(2),F(6)}.
则M(a)= ![]()
【解析】(1)由a≥3,讨论x≤1时,x>1,去掉绝对值,化简x2﹣2ax+4a﹣2﹣2|x﹣1|,判断符号,即可得到F(x)=x2﹣2ax+4a﹣2成立的x的取值范围;(2)(i)设f(x)=2|x﹣1|,g(x)=x2﹣2ax+4a﹣2,求得f(x)和g(x)的最小值,再由新定义,可得F(x)的最小值;(ii)分别对当0≤x≤2时,当2<x≤6时,讨论F(x)的最大值,即可得到F(x)在[0,6]上的最大值M(a).
【考点精析】认真审题,首先需要了解函数的最值及其几何意义(利用二次函数的性质(配方法)求函数的最大(小)值;利用图象求函数的最大(小)值;利用函数单调性的判断函数的最大(小)值).


 名师点拨卷系列答案
名师点拨卷系列答案 英才计划期末调研系列答案
英才计划期末调研系列答案科目:高中数学 来源: 题型:
【题目】某高校共有15000人,其中男生10500人,女生4500人,为调查该校学生每周平均体育运动时间的情况,采用分层抽样的方法,收集300位学生每周平均体育运动时间的样本数据(单位:小时)
(1)应收集多少位女生样本数据?
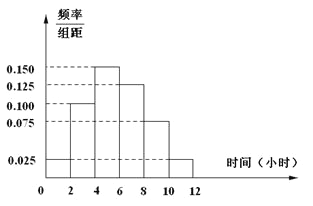
(2)根据这300个样本数据,得到学生每周平均体育运动时间的频率分布直方图(如图所示),其中样本数据分组区间为:![]() .估计该校学生每周平均体育运动时间超过4个小时的概率.
.估计该校学生每周平均体育运动时间超过4个小时的概率.
(3)在样本数据中,有60位女生的每周平均体育运动时间超过4个小时.请完成每周平均体育运动时间与性别的列联表,并判断是否有![]() 的把握认为“该校学生的每周平均体育运动时间与性别有关”.
的把握认为“该校学生的每周平均体育运动时间与性别有关”.
附:
![]()
| 0.10 | 0.05 | 0.010 | 0.005 |
| 2.706 | 3.841 | 6.635 | 7.879 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】学习雷锋精神前半年内某单位餐厅的固定餐椅经常有损坏,学习雷锋精神时全修好;单位对学习雷锋精神前后各半年内餐椅的损坏情况作了一个大致统计,具体数据如表:
损坏餐椅数 | 未损坏餐椅数 | 总计 | |
学习雷锋精神前 | 50 | 150 | 200 |
学习雷锋精神后 | 30 | 170 | 200 |
总计 | 80 | 320 | 400 |
![]() 求:学习雷锋精神前后餐椅损坏的百分比分别是多少?并初步判断损毁餐椅数量与学习雷锋精神是否有关?
求:学习雷锋精神前后餐椅损坏的百分比分别是多少?并初步判断损毁餐椅数量与学习雷锋精神是否有关?
![]() 请说明是否有
请说明是否有![]() 以上的把握认为损毁餐椅数量与学习雷锋精神
以上的把握认为损毁餐椅数量与学习雷锋精神
有关?![]() 参考公式:
参考公式:![]() ,
,
|
|
|
|
|
|
|
|
|
|
|
|
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】高三某班有60名学生(其中女生有20名),三好学生占![]() ,而且三好学生中女生占一半,现在从该班任选一名学生参加座谈会,则在已知没有选上女生的条件下,选上的是三好学生的概率是( )
,而且三好学生中女生占一半,现在从该班任选一名学生参加座谈会,则在已知没有选上女生的条件下,选上的是三好学生的概率是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某种植园在芒果临近成熟时,随机从一些芒果树上摘下100个芒果,其质量(单位:克)分别在![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 中,经统计得频率分布直方图如图所示.
中,经统计得频率分布直方图如图所示.

(1)现按分层抽样从质量为![]() ,
,![]() 的芒果中随机抽取6个,再从这6个中随机抽取3个,求这3个芒果中恰有1个在
的芒果中随机抽取6个,再从这6个中随机抽取3个,求这3个芒果中恰有1个在![]() 内的概率;
内的概率;
(2)某经销商来收购芒果,以各组数据的中间数代表这组数据的平均值,用样本估计总体,该种植园中还未摘下的芒果大约还有10000个,经销商提出如下两种收购方案:
![]() 方案:所有芒果以10元/千克收购;
方案:所有芒果以10元/千克收购;
![]() 方案:对质量低于250克的芒果以2元/个收购,高于或等于250克的以3元/个收购.
方案:对质量低于250克的芒果以2元/个收购,高于或等于250克的以3元/个收购.
通过计算确定种植园选择哪种方案获利更多?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4—4:坐标系与参数方程
平面直角坐标系xOy中,曲线C:![]() .直线l经过点P(m,0),且倾斜角为
.直线l经过点P(m,0),且倾斜角为![]() .O为极点,以x轴正半轴为极轴,建立极坐标系.
.O为极点,以x轴正半轴为极轴,建立极坐标系.
(Ⅰ)写出曲线C的极坐标方程与直线l的参数方程;
(Ⅱ)若直线l与曲线C相交于A,B两点,且|PA|·|PB|=1,求实数m的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com