
【题目】已知不等式x2﹣x﹣m+1>0.
(1)当m=3时解此不等式;
(2)若对于任意的实数x,此不等式恒成立,求实数m的取值范围.
【答案】
(1)解:当m=3时,
不等式x2﹣x﹣2>0
解得:x∈(﹣∞,﹣1)∪(2,+∞)
(2)解:设y=x2﹣x﹣m+1
∵不等式x2﹣x﹣m+1>0对于任意的x都成立
∴对x∈R,y>0恒成立
∴△=12+4(m﹣1)<0
∴ ![]()
故实数m的取值范围 ![]()
【解析】(1)当m=3时,不等式x2﹣x﹣2>0,解可得答案;(2)不等式x2﹣x﹣m+1>0对任意实数x恒成立,设y=x2﹣x﹣m+1,再利用大于0恒成立须满足的条件:开口向上,判别式小于0来解m的取值范围.
【考点精析】本题主要考查了解一元二次不等式的相关知识点,需要掌握求一元二次不等式![]()
![]() 解集的步骤:一化:化二次项前的系数为正数;二判:判断对应方程的根;三求:求对应方程的根;四画:画出对应函数的图象;五解集:根据图象写出不等式的解集;规律:当二次项系数为正时,小于取中间,大于取两边才能正确解答此题.
解集的步骤:一化:化二次项前的系数为正数;二判:判断对应方程的根;三求:求对应方程的根;四画:画出对应函数的图象;五解集:根据图象写出不等式的解集;规律:当二次项系数为正时,小于取中间,大于取两边才能正确解答此题.


科目:高中数学 来源: 题型:
【题目】在△ABC中,内角A、B、C的对边分别是a、b、c,且b2+c2﹣a2=bc.
(1)求A;
(2)若a= ![]() ,sinBsinC=sin2A,求△ABC的周长.
,sinBsinC=sin2A,求△ABC的周长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】省环保研究所对某市市中心每天环境放射性污染情况进行调查研究后,发现一天中环境综合放射性污染指数![]() 与时刻
与时刻![]() (时)的关系为
(时)的关系为 ,其中
,其中![]() 是与气象有关的参数,且
是与气象有关的参数,且![]() ,若用每天
,若用每天![]() 的最大值为当天的综合放射性污染指数,并记作
的最大值为当天的综合放射性污染指数,并记作![]() .
.
(1)令![]() .求
.求![]() 的取值范围;
的取值范围;
(2)求![]() ;
;
(3)省政府规定,每天的综合放射性污染指数不得超过2,试问目前该市市中心的综合放射性污染指数是否超标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】市环保局举办2013年“六五”世界环境日宣传活动,进行现场抽奖.抽奖规则是:盒中装有10张大小相同的精美卡片,卡片上分别印有“环保会徽”或“绿色环保标志”图案.参加者每次从盒中抽取卡片两张,若抽到两张都是“绿色环保标志”卡即可获奖.
(1)活动开始后,一位参加者问:盒中有几张“绿色环保标志”卡?主持人笑说:我只知道若从盒中抽两张都不是“绿色环保标志”卡的概率是 ![]() .求抽奖者获奖的概率;
.求抽奖者获奖的概率;
(2)现有甲乙丙丁四人依次抽奖,抽后放回,另一人再抽.用ξ表示获奖的人数.求ξ的分布列及E(ξ),D(ξ).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,正三棱柱![]() 的各条棱长均相等,
的各条棱长均相等, ![]() 为
为![]() 的中点,
的中点, ![]() 分别是线段
分别是线段![]() 和线段
和线段![]() 上的动点(含端点),且满足
上的动点(含端点),且满足![]() .当
.当![]() 运动时,下列结论中不正确的是( )
运动时,下列结论中不正确的是( )
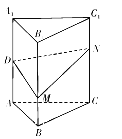
A. 平面![]() 平面
平面![]() B. 三棱锥
B. 三棱锥![]() 的体积为定值
的体积为定值
C. ![]() 可能为直角三角形 D. 平面
可能为直角三角形 D. 平面![]() 与平面
与平面![]() 所成的锐二面角范围为
所成的锐二面角范围为![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】解答题
(1)(1)已知命题p:|x2﹣x|≥6,q:x∈Z且“p且q”与“非q”同时为假命题,求x的值.
(2)已知p:x2﹣8x﹣20≤0,q:x2﹣2x+1﹣m2≤0(m>0),若¬p是¬q的必要而不充分条件,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,椭圆C: ![]() =1(a>b>0)的离心率为
=1(a>b>0)的离心率为 ![]() ,以原点为圆心,椭圆C的短半轴长为半径的圆与直线x﹣y+2=0相切.
,以原点为圆心,椭圆C的短半轴长为半径的圆与直线x﹣y+2=0相切. 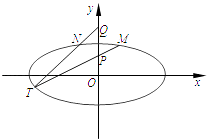
(1)求椭圆C的方程;
(2)已知点P(0,1),Q(0,2).设M,N是椭圆C上关于y轴对称的不同两点,直线PM与QN相交于点T,求证:点T在椭圆C上.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某保险公司有一款保险产品的历史收益率(收益率=利润÷保费收入)的频率分布直方图如图所示:

(Ⅰ)试估计平均收益率;
(Ⅱ)根据经验,若每份保单的保费在20元的基础上每增加![]() 元,对应的销量
元,对应的销量![]() (万份)与
(万份)与![]() (元)有较强线性相关关系,从历史销售记录中抽样得到如下5组
(元)有较强线性相关关系,从历史销售记录中抽样得到如下5组![]() 与
与![]() 的对应数据:
的对应数据:

据此计算出的回归方程为![]() .
.
(i)求参数![]() 的估计值;
的估计值;
(ii)若把回归方程![]() 当作
当作![]() 与
与![]() 的线性关系,用(Ⅰ)中求出的平均收益率估计此产品的收益率,每份保单的保费定为多少元时此产品可获得最大收益,并求出该最大收益.
的线性关系,用(Ⅰ)中求出的平均收益率估计此产品的收益率,每份保单的保费定为多少元时此产品可获得最大收益,并求出该最大收益.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com