练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    甲、乙、丙三名音乐爱好者参加某电视台举办的演唱技能海选活动，在本次海选中有合格和不合格两个等级．若海选合格记分，海选不合格记分．假设甲、乙、丙海选合格的概率分别为，他们海选合格与不合格是相互独立的．
    （1）求在这次海选中，这三名音乐爱好者至少有一名海选合格的概率；
    （2）记在这次海选中，甲、乙、丙三名音乐爱好者所得分之和为随机变量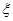,求随机变量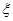的分布列和数学期望．

    （1） （2）

    解析试题分析：概率与统计类解答题是高考常考的题型，以排列组合和概率统计等知识为工具，主要考查对概率事件的判断及其概率的计算，随机变量概率分布列的性质及其应用：对于（1），从所求事件的对立事件的概率入手即；对于（2），根据的所有可能取值：0，1，2，3；分别求出相应事件的概率Ｐ，列出分布列，运用数学期望计算公式求解即可.
    （1）记“甲海选合格”为事件Ａ，“乙海选合格”为事件Ｂ，“丙海选合格”为事件Ｃ，“甲、乙、丙至少有一名海选合格”为事件Ｅ．
    ．
    （2）的所有可能取值为0,1,2,3．；
    ；
    ；
    ．
    所以的分布列为


    		0
    		1
    		2
    		3





     
    ．
    考点：离散型随机变量的概率、分布列和数学期望.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：解答题

    某校研究性学习小组从汽车市场上随机抽取20辆纯电动汽车调查其续驶里程（单次充电后能行驶的最大里程），被调查汽车的续驶里程全部介于50公里和300公里之间，将统计结果分成5组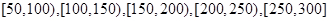：，绘制成如图所示的频率分布直方图.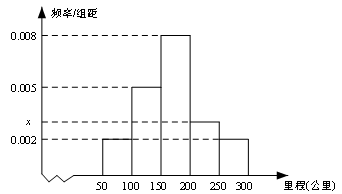

    （1）求直方图中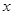的值；
    （2）求续驶里程在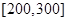的车辆数；
    （3）若从续驶里程在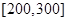的车辆中随机抽取2辆车，求其中恰有一辆车的续驶里程为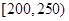的概率.

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    某射手进行射击训练，假设每次射击击中目标的概率为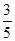，且每次射击的结果互不影响，已知射手射击了5
    次，求：
    (1)其中只在第一、三、五次击中目标的概率；
    (2)其中恰有3次击中目标的概率．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    某花店每天以每枝5元的价格从农场购进若干枝玫瑰花，然后以每枝10元的价格出售．如果当天卖不完，剩下的玫瑰花作垃圾处理．
    (1)若花店一天购进17枝玫瑰花，求当天的利润y(单位：元)关于当天需求量n(单位：枝，n∈N)的函数解析式；
    (2)花店记录了100天玫瑰花的日需求量(单位：枝)，整理得下表：

    日需求量n
    		14
    		15
    		16
    		17
    		18
    		19
    		20
    频数
    		10
    		20
    		16
    		16
    		15
    		13
    		10
     
    ①假设花店在这100天内每天购进17枝玫瑰花，求这100天的日利润(单位：元)的平均数；
    ②若花店一天购进17枝玫瑰花，以100天记录的各需求量的频率作为各需求量发生的概率，求当天的利润不少于75元的概率．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    （本小题满分12分）
    根据世行2013年新标准，人均GDP低于1035美元为低收入国家；人均GDP为1035-4085元为中等偏下收入国家；人均GDP为4085-12616美元为中等偏上收入国家；人均GDP不低于12616美元为高收入国家.某城市有5个行政区，各区人口占该城市人口比例及人均GDP如下表：

    （1）判断该城市人均GDP是否达到中等偏上收入国家标准；
    （2）现从该城市5个行政区中随机抽取2个，求抽到的2个行政区人均GDP都达到中等偏上收入国家标准的概率.

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    某电视台在一次对收看文艺节目和新闻节目观众的抽样调查中，随机抽取了100名电视观众，相关的数据如下表所示：

     
    		文艺节目
    		新闻节目
    		总计
    20至40岁
    		40
    		18
    		58
    大于40岁
    		15
    		27
    		42
    总计
    		55
    		45
    		100
     
    (1)由表中数据直观分析，收看新闻节目的观众是否与年龄有关？
    (2)用分层抽样方法在收看新闻节目的观众中随机抽取5名，大于40岁的观众应该抽取几名？
    (3)在上述抽取的5名观众中任取2名，求恰有1名观众的年龄为20至40岁的概率．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    李明在10场篮球比赛中的投篮情况统计如下（假设各场比赛相互独立）：

    场次
    		投篮次数
    		命中次数
    		场次
    		投篮次数
    		命中次数
    主场1
    		22
    		12
    		客场1
    		18
    		8
    主场2
    		15
    		12
    		客场2
    		13
    		12
    主场3
    		12
    		8
    		客场3
    		21
    		7
    主场4
    		23
    		8
    		客场4
    		18
    		15
    主场5
    		24
    		20
    		客场5
    		25
    		12
     
    （1）从上述比赛中随机选择一场，求李明在该场比赛中投篮命中率超过0.6的概率；
    （2）从上述比赛中随机选择一个主场和一个客场，求李明的投篮命中率一场超过0.6，一场不超过0.6的概率；
    （3）记为表中10个命中次数的平均数，从上述比赛中随机选择一场，记为李明在这场比赛中的命中次数，比较与的大小（只需写出结论）

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    甲、乙两个篮球运动员互不影响地在同一位置投球，命中率分别为与，且乙投球次均未命中的概率为．
    （1）求乙投球的命中率；
    （2）若甲投球次，乙投球次，两人共命中的次数记为，求的分布列和数学期望．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    已知复数z＝x＋yi(x，y∈R)在复平面上对应的点为M．
    (1)设集合P＝{－4，－3，－2,0}，Q＝{0,1,2}，从集合P中随机取一个数作为x，从集合Q中随机取一个数作为y，求复数z为纯虚数的概率；
    (2)设x∈[0,3]，y∈[0,4]，求点M落在不等式组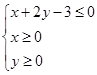：所表示的平面区域内的概率．

    查看答案和解析>>

    同步练习册答案