
分析 求出圆心到直线的距离与半径比较,解不等式、方程,即可得出结论.
解答 解:圆x2+y2-6x+5=0可化为圆(x-3)2+y2=4,圆心为(3,0),半径为2.圆心到直线的距离d=$\frac{6}{\sqrt{1+{m}^{2}}}$
(1)d=$\frac{6}{\sqrt{1+{m}^{2}}}$<2,可得m<-2$\sqrt{2}$或m>2$\sqrt{2}$,直线与圆相交;
(2)d=$\frac{6}{\sqrt{1+{m}^{2}}}$=2,可得m=-2$\sqrt{2}$或m=2$\sqrt{2}$,直线与圆相切;
(3)d=$\frac{6}{\sqrt{1+{m}^{2}}}$>2,可得-2$\sqrt{2}$<m<2$\sqrt{2}$,直线与圆相离.
点评 本题考查直线与圆的位置关系,考查学生的计算能力,正确求出圆心到直线的距离是关键.


 53随堂测系列答案
53随堂测系列答案科目:高中数学 来源: 题型:选择题
| A. | [-1,+∞) | B. | [-1,0)∪(3,+∞) | C. | (-∞,-1]∪(1,+∞) | D. | (-∞,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [-3,3] | B. | {-3,3} | C. | (-3,3) | D. | (-∞,-3]∪[3,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 与两坐标轴相切 | B. | 与两坐标轴均不相交 | ||
| C. | 与坐标轴上截得不相等的线段 | D. | 在坐标轴上截得相等的线段 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
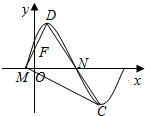 如图是函数f(x)=Asin(ωx+φ)(A>0,ω>0,0<φ<$\frac{π}{2}$)的部分图象,M、N是它与x轴的两个交点,D、C分别为它的最高点和最低点,点F(0,1)是线段MD的中点,$\overrightarrow{MD}$•$\overrightarrow{MN}$=$\frac{{π}^{2}}{18}$.
如图是函数f(x)=Asin(ωx+φ)(A>0,ω>0,0<φ<$\frac{π}{2}$)的部分图象,M、N是它与x轴的两个交点,D、C分别为它的最高点和最低点,点F(0,1)是线段MD的中点,$\overrightarrow{MD}$•$\overrightarrow{MN}$=$\frac{{π}^{2}}{18}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com