
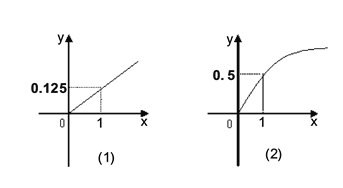
����Ŀ��ij��ͥ��������Ͷ�ʣ����ݳ����������г�Ԥ�⣬Ͷ��ծȯ���Ƚ��Ͳ�Ʒ��һ��������Ͷ�ʶ�����ȣ����ϵ��ͼ(1)��Ͷ�ʹ�Ʊ�ȷ����Ͳ�Ʒ��һ��������Ͷ�ʶ������ƽ���������ȣ����ϵ��ͼ(2).��ע��������Ͷ�ʶλ����Ԫ��
(1)�ֱ�д�����ֲ�Ʒ��һ��������Ͷ�ʶ�ĺ�����ϵ��
(2)�ü�ͥ����20��Ԫ�ʽ�ȫ����������Ͷ�ʣ��ʣ���ô�����ʽ���ʹһ���Ͷ�ʻ��������棬����������Ƕ�����Ԫ��
���𰸡���1��![]() ��
�� ![]() ��2����
��2����![]() ��Ԫ
��Ԫ
�������������������1������ͼ��д������![]() ���ֱ�
���ֱ�![]() �����Ӧ�����������
�����Ӧ�����������![]() ��ֵ���õ�������ϵʽ��2��������֪����д����Ͷ������ķ���
��ֵ���õ�������ϵʽ��2��������֪����д����Ͷ������ķ���![]() ������ת��Ϊ����
������ת��Ϊ����![]() ��ͨ��
��ͨ��![]() ��ȡֵ��Χ���
��ȡֵ��Χ���![]() ��ȡֵ��Χ�����������
��ȡֵ��Χ�����������![]() �����ֵ.
�����ֵ.
���������
(1)��![]() ��
�� ![]() ��
��
���� ![]() ��
�� ![]() ��
��
��![]() ��
�� ![]() ��
��
(2)��Ͷ��ծȯ���Ʒ![]() ��Ԫ�����Ʊ��Ͷ��Ϊ
��Ԫ�����Ʊ��Ͷ��Ϊ![]() ��Ԫ��
��Ԫ��
������ã� ![]()
![]()
![]() ��
��
��![]()
![]() ����
����![]()
![]() ��
��
���Ե�![]() ����
����![]() ��Ԫʱ���������
��Ԫʱ��������� ![]() ��Ԫ��
��Ԫ��


 �����������һ��һ��ϵ�д�
�����������һ��һ��ϵ�д� Ӧ������ҵ��ϵ�д�
Ӧ������ҵ��ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ԲC���㣺�ٽ�y�������ҳ�Ϊ2���ڱ�x��ֳ�����Բ�����仡���ı�Ϊ3:1�������������١��ڵ�����Բ�У���Բ�ĵ�ֱ��l:x-2y=0�ľ�����С��Բ�ķ��̣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����![]() ��
��
(1)������![]() �ڵ�
�ڵ�![]() ����������ֱ��
����������ֱ��![]() ��ֱ����ʵ��
��ֱ����ʵ��![]() ��ֵ��
��ֵ��
(2)���ۺ���![]() �ĵ����ԣ�
�ĵ����ԣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijͬѧ�á���㷨��������f��x��=Asin����x+![]() �����أ�0��|
�����أ�0��|![]() |��
|��![]() ����ijһ�������ڵ�ͼ��ʱ���б��������˲������ݣ������
����ijһ�������ڵ�ͼ��ʱ���б��������˲������ݣ������
��x+�� | 0 |
| �� |
| 2�� |
x |
|
| |||
Asin(��x+�գ� | 0 | 2 | -2 | 0 |
��1���뽫�ϱ����ݲ�����������д�ڴ��������Ӧλ�ã���ֱ��д������f��x���Ľ���ʽ��
��2����f��![]() ��=
��=![]() ����cos��2��+
����cos��2��+![]() ����ֵ��
����ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ֱ������ABC��A1B1C1�У���BAC=90�㣬AB=AC=AA1=1���ӳ�A1C1����P��ʹC1P=A1C1 �� ����AP����CC1�ڵ�D�� ������֤��PB1��ƽ��BDA1��
����������A��A1D��B��ƽ��ǵ�����ֵ��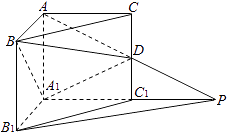
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���躯��f��x��=|2x��a|�� ������a=4����f��x����x�Ľ⼯��
������f��x+1����|2��a|��x�ʣ�0��+�ޣ����������ʵ��a��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����![]() ��
��
��1����![]() ʱ��������
ʱ��������![]() �ڵ�
�ڵ�![]() �������߷��̣�
�������߷��̣�
��2���ڣ�1���������£���֤��![]() ��
��
��3����![]() ʱ������
ʱ������![]() ��
��![]() �ϵ����ֵ��
�ϵ����ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����������ĸ�����
![]() ����
����![]() �����ֵΪ
�����ֵΪ![]() ��
��
![]() ��֪����
��֪����![]() ��
��![]() ��
��![]() ���Ǽ���������a��ȡֵ��Χ��
���Ǽ���������a��ȡֵ��Χ��![]() ��
��
![]() ��ͬһ����ϵ�У�����
��ͬһ����ϵ�У�����![]() ��
��![]() ��ͼ�����y��Գƣ�
��ͼ�����y��Գƣ�
![]() ��ͬһ����ϵ�У�����
��ͬһ����ϵ�У�����![]() ��
��![]() ��ͼ�����ֱ��
��ͼ�����ֱ��![]() �Գƣ�
�Գƣ�
������ȷ���۵������______��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊ��ǿѧ������,ѧУ��֯��������,ij������4�˻��������μ��������������,ÿ��ֻ�ܴ�����������ѡ������һ������,���Լ��:ÿ����ͨ����һö�ʵؾ��ȵ����Ӿ����Լ��μ��ĸ�����,��������Ϊ5��6���˲μ���������,��������С��5���˲μ���������.
(��)����4����ǡ��1�˲μ��������ŵĸ��ʣ�
(��)��![]() �ֱ��ʾ��4���вμ��������ź��������ŵ�����,���������
�ֱ��ʾ��4���вμ��������ź��������ŵ�����,���������![]() Ϊ
Ϊ![]() ��
��![]() �ij˻�,���������
�ij˻�,���������![]() �ķֲ�������ѧ����
�ķֲ�������ѧ����![]() .
.
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com